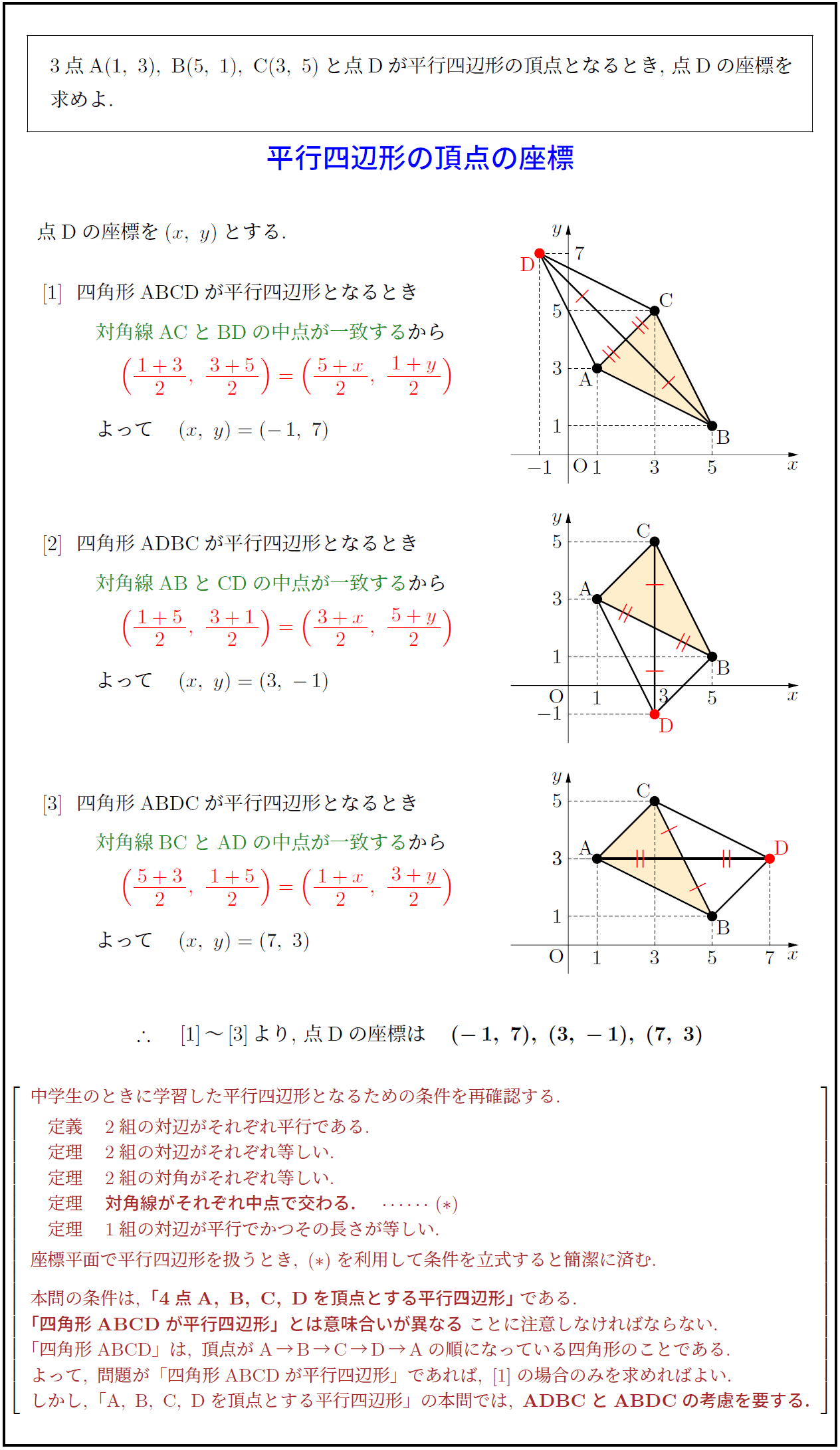
3点$\mathRM{A(1,\ 3),\ B(5,\ 1),\ C(3,\ 5)}$と点Dが平行四辺形の頂点となるとき,\ 点Dの座標を 平行四辺形の頂点の座標}}}} \\\\[.5zh] 点Dの座標を$(x,\ y)$とする. \\\\ [1]\ \ 四角形ABCDが平行四辺形となるとき{対角線ACとBDの中点が一致する}から \\ [2]\ \ 四角形ADBCが平行四辺形となるとき 対角線ABとCDの中点が一致する}から [3]\ \ 四角形ABDCが平行四辺形となるとき \対角線BCとADの中点が一致する}から 中学生のときに学習した平行四辺形となるための条件を再確認する. \\[.5zh] 定義 2組の対辺がそれぞれ平行である. \\[.2zh] 定理 2組の対辺がそれぞれ等しい. \\[.2zh] 定理 2組の対角がそれぞれ等しい. \\[.2zh] 定理 \bm{対角線がそれぞれ中点で交わる.} \cdots\cdots\,(*) \\[.2zh] 定理 1組の対辺が平行でかつその長さが等しい. \\[.5zh] 座標平面で平行四辺形を扱うとき,\ (*)を利用して条件を立式すると簡潔に済む. \\[1zh] 本問の条件は,\ \bm{「4点\mathRM{A,\ B,\ C,\ D}を頂点とする平行四辺形」}である. \\[.2zh] \bm{「四角形\mathRM{ABCD}が平行四辺形」とは意味合いが異なる}ことに注意しなければならない. \\[.2zh] 「四角形\mathRM{ABCD}」は,\ 頂点が\mathRM{A\,→\,B\,→\,C\,→\,D\,→\,A}の順になっている四角形のことである. \\[.2zh] よって,\ 問題が「四角形\mathRM{ABCD}が平行四辺形」であれば,\ [1]の場合のみを求めればよい. \\[.2zh] しかし,\ 「\mathRM{A,\ B,\ C,\ D}を頂点とする平行四辺形」の本問では,\ \bm{\mathRM{ADBCとABDC}の考慮を要する.
