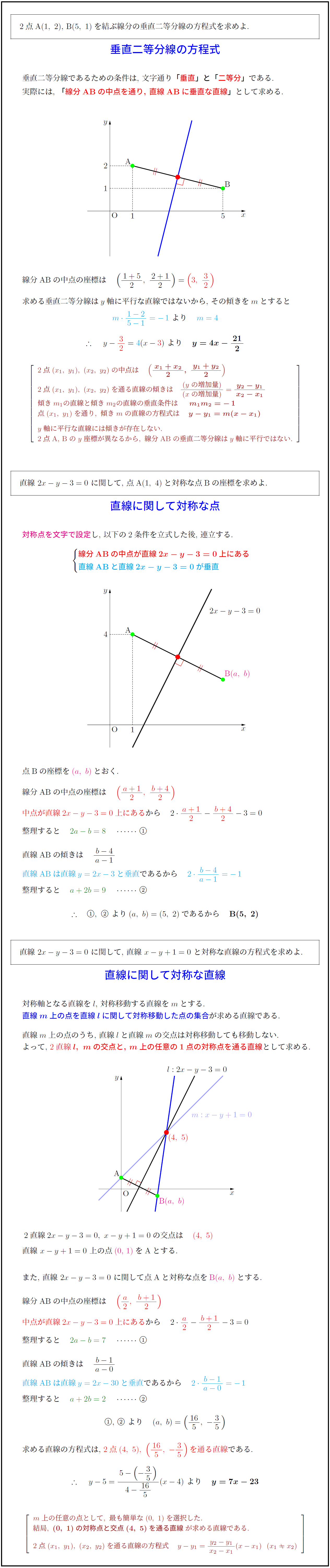
2点A$(1,\ 2)$,\ B$(5,\ 1)$を結ぶ線分の垂直二等分線の方程式を求めよ. \\
垂直二等分線の方程式 \\
垂直二等分線であるための条件は,\ 文字通り「垂直}」と「二等分}」}である.
実際には,\{線分ABの中点を通り,\ 直線ABに垂直な直線}」}として求める.
求める垂直二等分線は$y$軸に平行な直線ではないから,\ その傾きを$m$とすると
2点(x_1,\ y_1),\ (x_2,\ y_2)を通る直線の傾きは (yの増加量)}{(xの増加量)}=y_2-y_1}{x_2-x_1
傾きm_1の直線と傾きm_2の直線の垂直条件は\ m_1m_2=-\,1}
点(x_1,\ y_1)を通り,\ 傾きmの直線の方程式は y-y_1=m(x-x_1)}
y軸に平行な直線には傾きが存在しない.
2点A,\ B}のy座標が異なるから,\ 線分AB}の垂直二等分線はy軸に平行ではない.
直線\ $2x-y-3=0$\ に関して,\ 点A$(1,\ 4)$と対称な点Bの座標を求めよ. \\
直線に関して対称な点{対称点を文字で設定し,\ 以下の2条件を立式した後,\ 連立する.
線分AB}の中点が直線2x-y-3=0上にある}
直線AB}と直線2x-y-3=0が垂直}
点Bの座標を$(a,\ b)}$とおく.
線分ABの中点の座標は
中点が直線$2x-y-3=0$上にある}から
直線ABの傾きは $b-4}{a-1}$
直線ABは直線$y=2x-3$と垂直}であるから $
直線\ $2x-y-3=0$\ に関して,\ 直線\ $x-y+1=0$\ と対称な直線の方程式を求めよ. \\
直線に関して対称な直線 \\
対称軸となる直線を$l$,\ 対称移動する直線を$m$とする. \\
直線$m}$上の点を直線$l}$に関して対称移動した点の集合が求める直線である.
直線$m$上の点のうち,\ 直線$l$と直線$m$の交点は対称移動しても移動しない. \\
よって,\ $2直線l,\ m}$の交点と,\ $m}$上の任意の1点の対称点を通る直線として求める.
2直線$2x-y-3=0,\ x-y+1=0$の交点は $(4,\ 5)}$
直線\ $x-y+1=0$\ 上の点(0,\ 1)}をAとする.
また,\ 直線\ $2x-y-3=0$\ に関して点Aと対称な点をB$(a,\ b)$}とする.
線分ABの中点の座標は $a}{2},\ b+1}{2$
中点が直線$2x-y-3=0$上にある}から
直線ABの傾きは $b-1}{a-0}$
直線ABは直線$y=2x-30$と垂直}であるから $2・b-1}{a-0}=-\,1}$
整理すると
求める直線の方程式は,\ $2点(4,\ 5),\ 16}{5},\ -35を通る直線}である.
m上の任意の点として,\ 最も簡単な(0,\ 1)を選択した.
結局,\ (0,\ 1)の対称点と交点(4,\ 5)を通る直線}が求める直線である.
2点(x_1,\ y_1),\ (x_2,\ y_2)を通る直線の方程式 y-y_1=y_2-y_1}{x_2-x_1}(x-x_1)\ \ (x_1≠ x_2)

