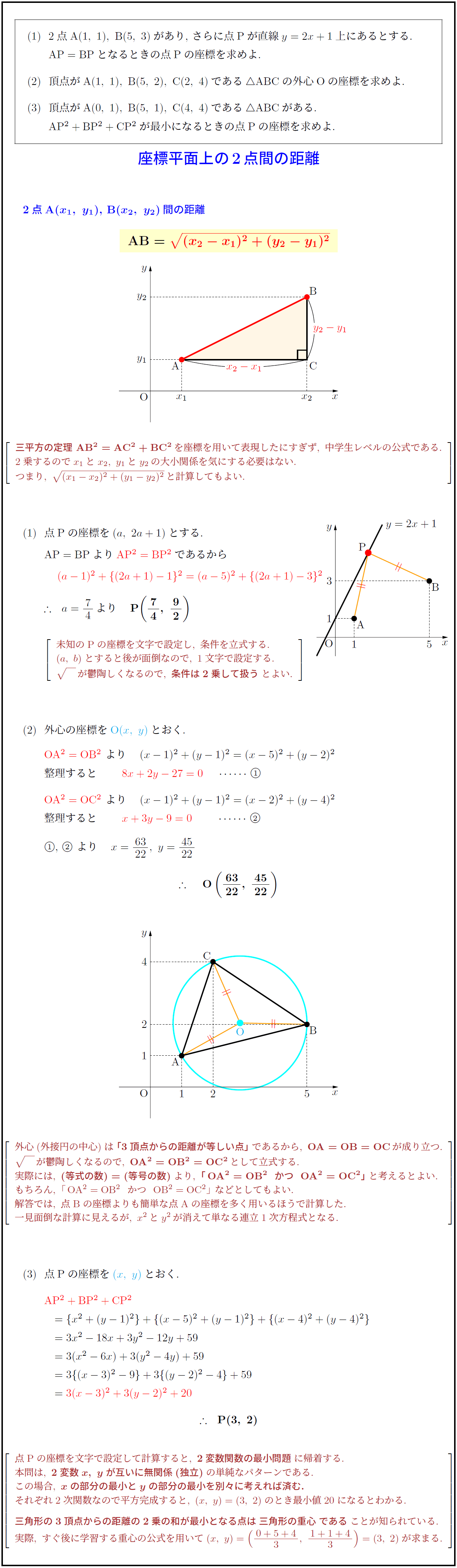
2点$\mathRM{A(1,\ 1),\ B(5,\ 3)}$があり,\ さらに点Pが直線$y=2x+1$上にあるとする. \\[.2zh] \hspace{.5zw}\phantom{(1)}\ \ $\mathRM{AP=BP}$となるときの点Pの座標を求めよ. \\[1zh] \hspace{.5zw}(2)\ \ 頂点が$\mathRM{A(1,\ 1),\ B(5,\ 2),\ C(2,\ 4)}$である$\triangle$ABCの外心Oの座標を求めよ. \\[1zh] \hspace{.5zw}(3)\ \ 頂点が$\mathRM{A(0,\ 1),\ B(5,\ 1),\ C(4,\ 4)}$である$\triangle$ABCがある. \\[.2zh] \hspace{.5zw}\phantom{(1)}\ \ $\mathRM{AP^2+BP^2+CP^2}$が最小になるときの点Pの座標を求めよ. \座標平面上の2点間の距離 \bm{三平方の定理\ \mathRM{AB^2=AC^2+BC^2}}\,を座標を用いて表現したにすぎず,\ 中学生レベルの公式である. \\[.2zh] 2乗するのでx_1\,とx_2,\ y_1\,とy_2\,の大小関係を気にする必要はない. \\[.2zh] つまり,\ \ruizyoukon{(x_1-x_2)^2+(y_1-y_2)^2}\,と計算してもよい. (1)\ \ 点Pの座標を$(a,\ 2a+1)$とする. \\[.5zh] \phantom{ (1)}\ \ $\mathRM{AP=BPより\textcolor{red}{AP^2=BP^2}}$であるから 未知の\text Pの座標を文字で設定し,\ 条件を立式する. \\[.2zh] (a,\ b)とすると後が面倒なので,\ 1文字で設定する. \\[.2zh] \ruizyoukon{ }\,が鬱陶しくなるので,\ \bm{条件は2乗して扱う}とよい. (2)\ \ 外心の座標を 外心(外接円の中心)は\bm{「3頂点からの距離が等しい点」}であるから,\ \bm{\mathRM{OA=OB=OC}}\,が成り立つ. \\[.2zh] \ruizyoukon{ }\,が鬱陶しくなるので,\ \bm{\mathRM{OA^2=OB^2=OC^2}}\,として立式する. \\[.2zh] 実際には,\ \bm{(等式の数)=(等号の数)}より,\ \bm{\mathRM{「\,OA^2=OB^2\ \ かつ\ \ OA^2=OC^2」}}と考えるとよい. \\[.2zh] もちろん,\ \mathRM{「\,OA^2=OB^2\ \ かつ\ \ OB^2=OC^2」}\ などとしてもよい. \\[.2zh] 解答では,\ \mathRM{点Bの座標よりも簡単な点Aの座標を多く用いるほうで計算した.} \\[.2zh] 一見面倒な計算に見えるが,\ x^2\,とy^2\,が消えて単なる連立1次方程式となる. 点\text Pの座標を文字で設定して計算すると,\ \bm{2変数関数の最小問題}に帰着する. \\[.2zh] 本問は,\ \bm{2変数x,\ yが互いに無関係(独立)}の単純なパターンである. \\[.2zh] この場合,\ \bm{xの部分の最小とyの部分の最小を別々に考えれば済む.} \\[.2zh] それぞれ2次関数なので平方完成すると,\ (x,\ y)=(3,\ 2)のとき最小値20になるとわかる. \\[1zh] \bm{三角形の3頂点からの距離の2乗の和が最小となる点は\bm{三角形の重心}である}ことが知られている. \\[.2zh] 実際,\ すぐ後に学習する重心の公式を用いて(x,\ y)=\left(\bunsuu{0+5+4}{3},\ \bunsuu{1+1+4}{3}\right)=(3,\ 2)が求まる.
