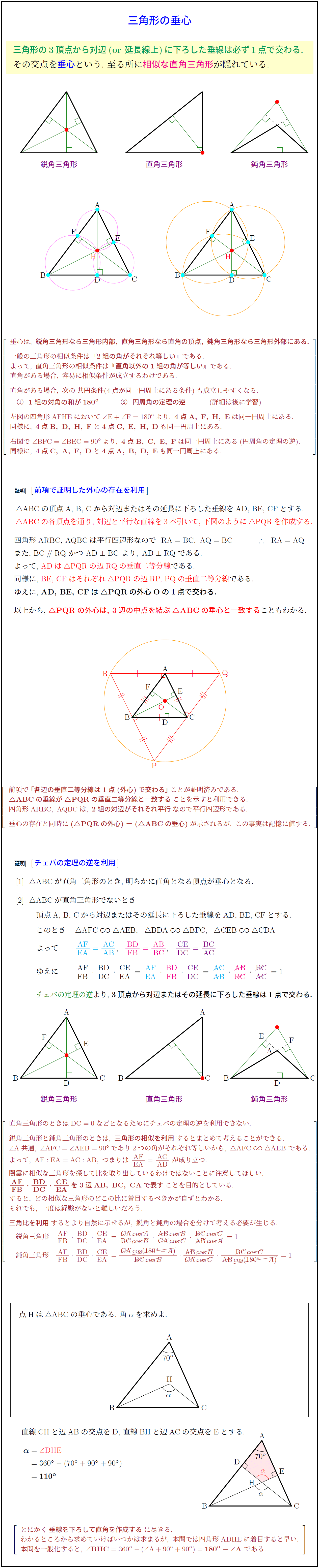
三角形の3頂点から対辺(or 延長線上)に下ろした垂線は必ず1点で交わる.
その交点を垂心という.\ 至る所に相似な直角三角形が隠れている.
{直角三角形}
垂心は,\ 鋭角三角形なら三角形内部,\ 直角三角形なら直角の頂点,\ 鈍角三角形なら三角形外部にある.}
一般の三角形の相似条件は『2組の角がそれぞれ等しい}』である.
よって,\ 直角三角形の相似条件は『直角以外の1組の角が等しい}』である.
直角がある場合,\ 容易に相似条件が成立するわけである.
直角がある場合,\ 次の共円条件}(4点が同一円周上にある条件)も成立しやすくなる.
①\ \ 1組の対角の和が180°} ②\ \ 円周角の定理の逆} (詳細は後に学習)
左図の四角形AFHEにおいて\ ∠ E+∠ F=180°}\,より,\ 4点A,\ F,\ H,\ Eは同一円周上にある.
同様に,\ 4点B,\ D,\ H,\ Fと4点C,\ E,\ H,\ Dも同一円周上にある.
右図で\ ∠ BFC=∠ BEC=90°}\,より,\ 4点B,\ C,\ E,\ Fは同一円周上にある(円周角の定理の逆).
同様に,\ 4点C,\ A,\ F,\ Dと4点A,\ B,\ D,\ Eも同一円周上にある.
前項で証明した外心の存在を利用\,]
$△$ABCの頂点A,\ B,\ Cから対辺またはその延長に下ろした垂線をAD,\ BE,\ CFとする.
$△$ABCの各頂点を通り,\ 対辺と平行な直線を3本引いて,\ 下図のように$△$PQRを作成する.}
四角形ARBC,\ AQBCは平行四辺形なので\ \ $RA=BC,\ AQ=BC ∴\ \ RA=AQ}$
また, $BC∥ RQ\ かつ\ AD⊥ BC\ より,\ AD⊥ RQ\ である.}$
よって,\ ADは$△$PQRの辺RQの垂直二等分線}である.
同様に,\ BE,\ CFはそれぞれ$△$PQRの辺RP,\ PQの垂直二等分線}である.
3辺の中点を結ぶ$△}$ABCの垂心と一致することもわかる
前項で「各辺の垂直二等分線は1点(外心)で交わる」}ことが証明済みである.
△ABC}の垂線が△PQR}の垂直二等分線と一致する}ことを示すと利用できる.
四角形ARBC,\ AQBC}は,\ 2組の対辺がそれぞれ平行}なので平行四辺形である.
垂心の存在と同時に(△ PQRの外心)=(△ ABCの垂心)が示されるが,\ この事実は記憶に値する.
チェバの定理の逆を利用\,]
[1]\ \ $△$ABCが直角三角形のとき,\ 明らかに直角となる頂点が垂心となる.
[2]\ \ $△$ABCが直角三角形でないとき
頂点A,\ B,\ Cから対辺またはその延長に下ろした垂線をAD,\ BE,\ CFとする.
チェバの定理の逆}より,\ 3頂点から対辺またはその延長に下ろした垂線は1点で交わる.
直角三角形のときはDC=0}などとなるためにチェバの定理の逆を利用できない.
鋭角三角形と鈍角三角形のときは,\ 三角形の相似を利用}するとまとめて考えることができる.
∠ A共通,\ ∠ AFC=∠ AEB=90°}\,であり2つの角がそれぞれ等しいから,\ △ AFC∽△ AEB}\ である.
よって,\ AF:EA=AC:AB},\ つまりは\ AF}{EA}=AC}{AB\ が成り立つ.
闇雲に相似な三角形を探して比を取り出しているわけではないことに注意してほしい.
AF}{FB}・BD}{DC}・CE}{EA\,を3辺AB,\ BC,\ CA}で表す}ことを目的としている.
すると,\ どの相似な三角形のどこの比に着目するべきかが自ずとわかる.
それでも,\ 一度は経験がないと難しいだろう.
三角比を利用}するとより自然に示せるが,\ 鋭角と鈍角の場合を分けて考える必要が生じる.
点Hは$△$ABCの垂心である.\ 角αを求めよ.
直線CHと辺ABの交点をD,\ 直線BHと辺ACの交点をEとする. \
とにかく垂線を下ろして直角を作成する}に尽きる.
わかるところから求めていけばいつかは求まるが,\ 本問では四角形ADHE}に着目すると早い.
本問を一般化する

