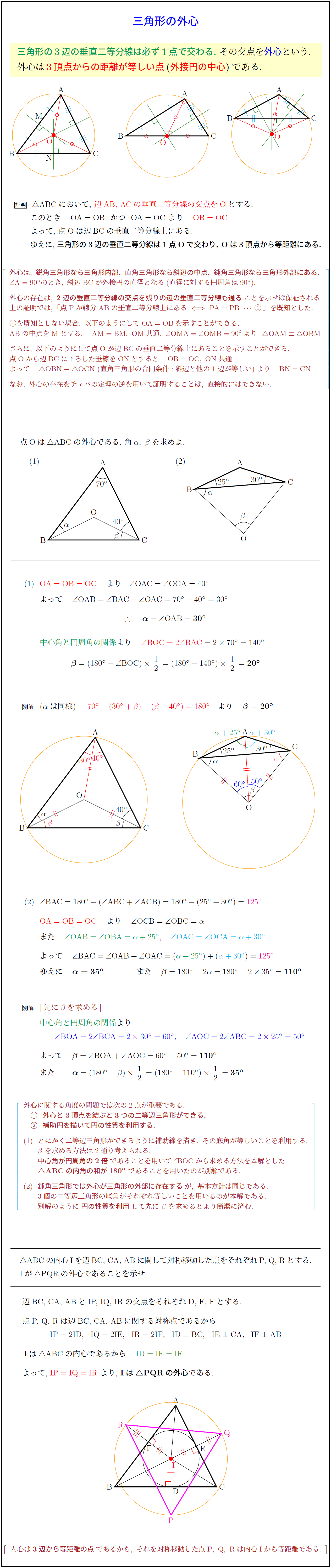
三角形の3辺の垂直二等分線は必ず1点で交わる.\ その交点を外心という.}
外心は3頂点からの距離が等しい点}(外接円の中心})}である.
辺AB,\ ACの垂直二等分線の交点をO}とする.
\ \ このとき $OA=OB\ \ かつ\ \ OA=OC\ より OB=OC$
\ \ よって,\ 点Oは辺BCの垂直二等分線上にある.
\ \ ゆえに,\ 三角形の3辺の垂直二等分線は1点Oで交わり,\ Oは3頂点から等距離にある
外心は,\ 鋭角三角形なら三角形内部,\ 直角三角形なら斜辺の中点,\ 鈍角三角形なら三角形外部にある.}
∠ A=90° のとき,\ 斜辺BCが外接円の直径となる(直径に対する円周角は90°).}
外心の存在は,\ 2辺の垂直二等分線の交点を残りの辺の垂直二等分線も通る}ことを示せば保証される.
上の証明では,\ 「点Pが線分ABの垂直二等分線上にある\ ⇔\ PA=PB}\ ・・・\,①\,」を既知とした.
①を既知としない場合,\ 以下のようにしてOA=OB}を示すことができる.
ABの中点をMとする. AM=BM,\ OM共通,\ ∠ OMA=∠ OMB=90°\,より\ \ △ OAM≡△ OBM}
さらに,\ 以下のようにして点Oが辺BCの垂直二等分線上にあることを示すことができる.}
点Oから辺BCに下ろした垂線をONとすると OB=OC,\ ON共通}
よって △ OBN≡ △ OCN\ (直角三角形の合同条件:斜辺と他の1辺が等しい)より BN=CN}
なお,\ 外心の存在をチェバの定理の逆を用いて証明することは,\ 直接的にはできない.
点Oは$△$ABCの外心である.\ 角$α,\ β$を求めよ.中心角と円周角の関係}より $
外心に関する角度の問題では次の2点が重要である.
①\ \ 外心と3頂点を結ぶと3つの二等辺三角形ができる.}
②\ \ 補助円を描いて円の性質を利用する.}
(1)\ \ とにかく二等辺三角形ができるように補助線を描き,\ その底角が等しいことを利用する.
\ \ β\ を求める方法は2通り考えられる.
\ \ 中心角が円周角の2倍}であることを用いて∠ BOC}から求める方法を本解とした.
\ \ △ABC}の内角の和が180°}\ であることを用いたのが別解である.
(2)\ \ 鈍角三角形では外心が三角形の外部に存在する}が,\ 基本方針は同じである.
\ \ 3個の二等辺三角形の底角がそれぞれ等しいことを用いるのが本解である.
\ \ 別解のように円の性質を利用}して先に\ β\ を求めるとより簡潔に済む.$△$ABCの内心Iを辺BC,\ CA,\ ABに関して対称移動した点をそれぞれP,\ Q,\ Rとする.
Iが$△$PQRの外心であることを示せ. \\
辺BC,\ CA,\ ABとIP,\ IQ,\ IRの交点をそれぞれD,\ E,\ Fとする.
点P,\ Q,\ Rは辺BC, CA, ABに関する対称点であるから
$IP=2ID,\ \ IQ=2IE,\ \ IR=2IF,\ \ ID⊥ BC,\ \ IE⊥ CA,\ \ IF⊥ AB}$}
Iは$△$ABCの内心であるから $ID=IE=IF$
よって,\ $IP=IQ=IR$\ より,\ Iは$△}$PQRの外心}である. \\

