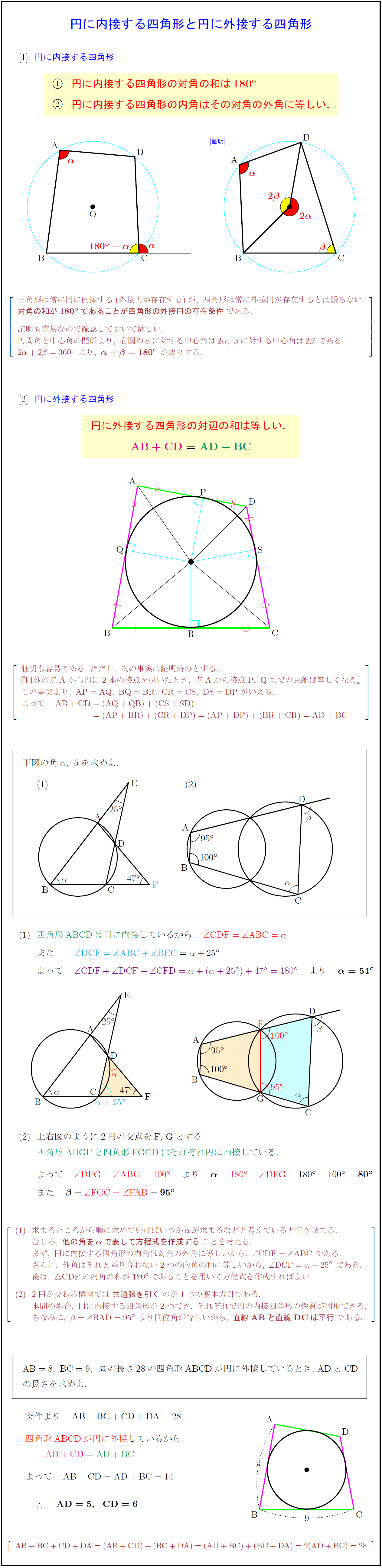
円に内接する四角形 円に内接する四角形の対角の和は${180°}$}{円に内接する四角形の内角はその対角の外角に等しい. 三角形は常に円に内接する(外接円が存在する)が,\ 四角形は常に外接円が存在するとは限らない. {対角の和が180°であることが四角形の外接円の存在条件}である. 証明も容易なので確認しておいて欲しい. 円周角と中心角の関係より,\ 右図のαに対する中心角は2α,\ βに対する中心角は2β\ である. 2α+2β=360°\ より,\ {α+β=180°}\ が成立する. 円に外接する四角形{円に外接する四角形の対辺の和は等しい. 証明も容易である.\ ただし,\ 次の事実は証明済みとする. 『円外の点 Aから円に2本の接点を引いたとき,\ 点{A}から接点{P,\ Q}までの距離は等しくなる』 この事実より, 上右図のように2円の交点をF,\ Gとする. 求まるところから順に求めていけばいつかαが求まるなどと考えていると行き詰まる. むしろ,\ {他の角をαで表して方程式を作成する}ことを考える. まず,\ 円に内接する四角形の内角は対角の外角に等しいから,\ {∠ CDF=∠ ABC}\ である. さらに,\ 外角はそれと隣り合わない2つの内角の和に等しいから,\ {∠ DCF=α+25°}\ である. 後は,\ { CDF}の内角の和が180°であることを用いて方程式を作成すればよい. 2円が交わる構図では{共通弦を引く}のが1つの基本方針である. 本問の場合,\ 円に内接する四角形が2つでき,\ それぞれで円の内接四角形の性質が利用できる. ちなみに,\ β={∠ BAD}=95°\ より同位角が等しいから,\ {直線{ABと直線DC}は平行}である. 周の長さ28の四角形ABCDが円に外接しているとき,\ ADとCD の長さを求めよ.

