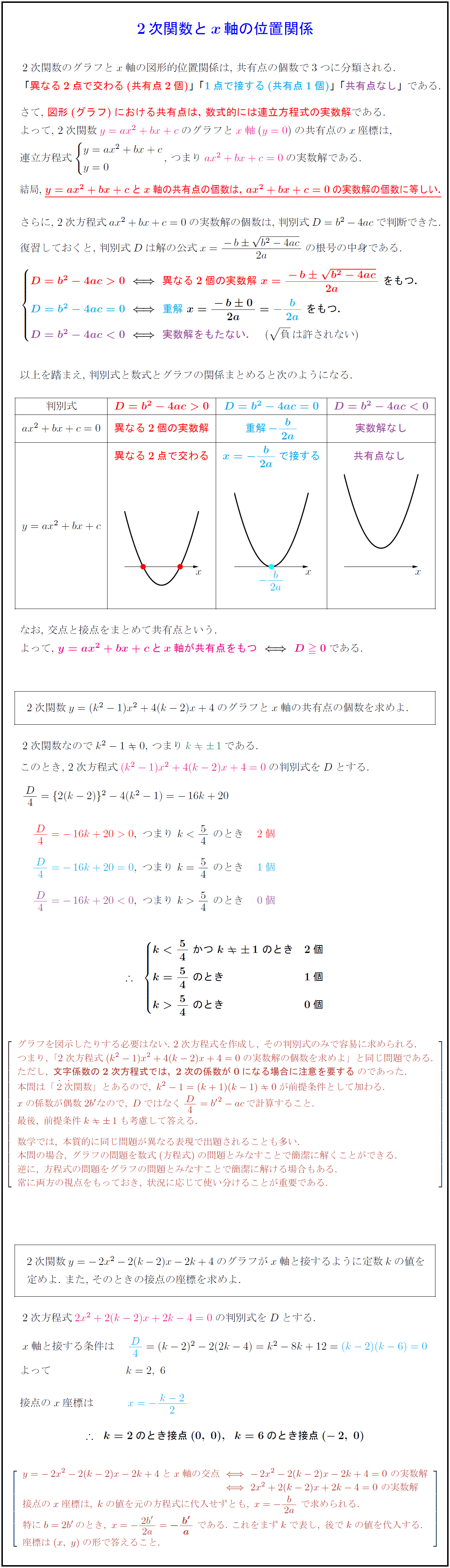
2次関数のグラフと$x$軸の図形的位置関係は,\ 共有点の個数で3つに分類される. 「異なる2点で交わる(共有点2個)}」「1点で接する(共有点1個)}」「共有点なし}」}である. さて,\ 図形(グラフ)における共有点は,\ 数式的には連立方程式の解である. よって,\ 2次関数$y=ax²+bx+c}$のグラフと$x$軸}($y=0}$)の共有点の$x$座標は, 連立方程式$ y=ax²+bx+c y=0 $-1zw},\ つまり$ax²+bx+c=0}$の実数解である. 0.92}{結局,\ ${y=ax²+bx+c}$と${x}$軸の共有点の個数は,\ ${ax²+bx+c=0}$の実数解の個数に等しい. さらに,\ 2次方程式$ax²+bx+c=0$の解の個数は,\ 判別式$D=b²-4ac$で判断できた. 復習しておくと,\ 判別式$D$は解の公式$x={-b{b²-4ac{2a}$の根号の中身である. $ {D=b²-4ac>0}異なる2個の実数解\ x={-b{b²-4ac{2a\ をもつ.} {D=b²-4ac=0}重解}\ x={-b0}{2a}=-{b}{2a\ をもつ.} {D=b²-4ac<0}実数解をもたない. ({負}は許されない) $} 以上を踏まえ,\ 判別式と数式とグラフの関係まとめると次のようになる. |c|c|c|c|} 判別式 & ${D=b²-4ac>0$ & ${D=b²-4ac=0$ & ${D=b²-4ac<0$ $ax²+bx+c=0$ & 異なる2個の実数解 & 重解${-{b}{2a$ & 実数解なし & 異なる2点で交わる & ${x=-{b}{2a$で接する & 共有点なし なお,\ 交点と接点をまとめて共有点という. よって,\ ${y=ax²+bx+cとx軸が共有点をもつ}\2次関数$y=(k²-1)x²+4(k-2)x+4$のグラフと$x$軸の共有点の個数を求めよ. [-.8zh] 2次関数なので$k²-10$,\ つまり$k1}$である. このとき,\ 2次方程式$(k²-1)x²+4(k-2)x+4=0}$の判別式を$D$とする. $ D4={2(k-2)}²-4(k²-1)=-16k+20$ $ D4=-16k+20>0},\ つまり\ k<54\ のとき 2個}$ グラフを図示したりする必要はない.\ 2次方程式を作成し,\ その判別式のみで容易に求められる. つまり,\ 「2次方程式(k²-1)x²+4(k-2)x+4=0の実数解の個数を求めよ.」と同じ問題である. ただし,\ {文字係数の2次方程式では,\ 2次の係数が0になる場合に注意を要する}のであった. 本問は「2}次}関数」とあるので,\ k²-1=(k+1)(k-1)0が前提条件として加わる. xの係数が偶数2b’なので,\ Dではなく D4={b’}²-acで計算すること. 最後,\ 前提条件k1も考慮して答える. 数学では,\ 本質的に同じ問題が異なる表現で出題されることも多い. 本問の場合,\ グラフの問題を数式(方程式)の問題とみなすことで簡潔に解くことができる. 逆に,\ 方程式の問題をグラフの問題とみなすことで簡潔に解ける場合もある. 常に両方の視点をもっておき,\ 状況に応じて使い分けることが重要である. 2次関数$y=-2x²-2(k-2)x-2k+4$のグラフが$x$軸と接するように定数$k$の値を 定めよ.\ また,\ そのときの接点の座標を求めよ. 2次方程式$2x²+2(k-2)x+2k-4=0}$の判別式を$D$とする. $x$軸と接する条件は $ D4}=(k-2)²-2(2k-4)=k²-8k+12=(k-2)(k-6)=0}$ よって $k=2,\ 6$ 接点の$x$座標は $x=-{k-2}{2$ ${k=2のとき接点(0,\ 0),k=6のとき接点(-2,\ 0)} y=-2x²-2(k-2)x-2k+4とx軸の交点-2x²-2(k-2)x-2k+4=0\ の実数解 {y=-2x²-2(k-2)x-2k+4とx軸の交点}2x²+2(k-2)x+2k-4=0\ の実数解 接点のx座標は,\ kの値を元の方程式に代入せずとも,\ x=-{b}{2a}\ で求められる. 特にb=2b’のとき,\ x=-{2b’}{2a}={-{b’}{a\ である.\ これをまずkで表し,\ 後でkの値を代入する. 座標は(x,\ y)の形で答えること.

