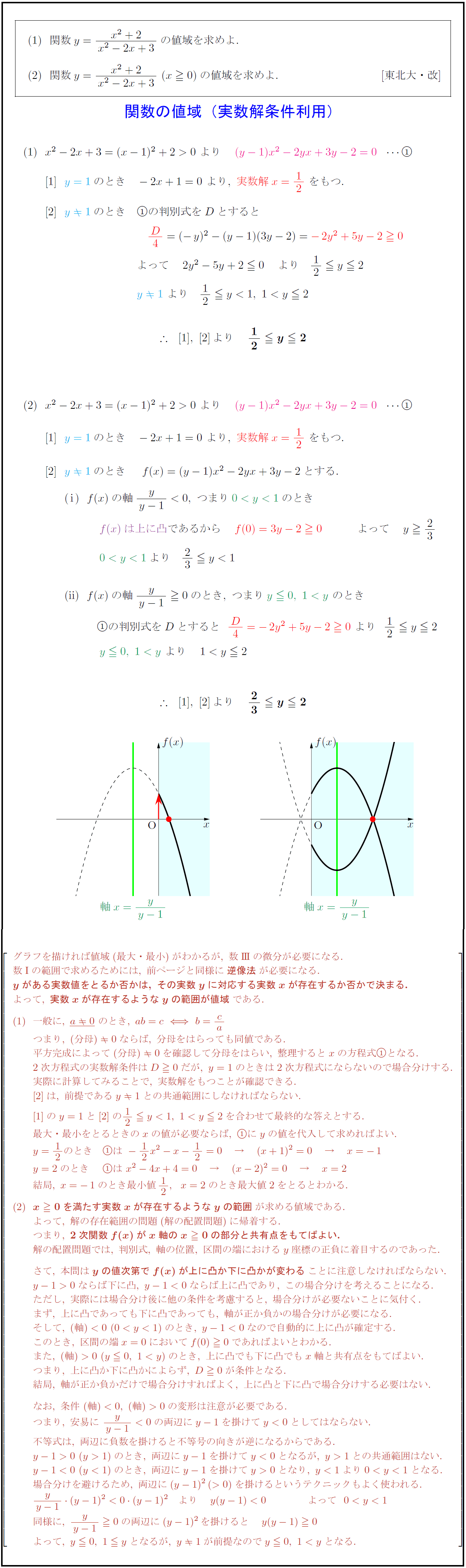
関数$y={x²+2}{x²-2x+3}$の値域を求めよ. 関数$y={x²+2}{x²-2x+3}\ (x0)$の値域を求めよ. [東北大・改] 関数の値域(実数解条件利用)実数解x= グラフを描ければ値域(最大・最小)がわかるが,\ 数III}の微分が必要になる. 数I}の範囲で求めるためには,\ 前ページと同様に{逆像法}が必要になる. {yがある実数値をとるか否かは,\ その実数yに対応する実数xが存在するか否かで決まる.} よって,\ {実数xが存在するようなyの範囲が値域}である. 一般に,\ a0}\ のとき,\ ab=cb= ca つまり,\ (分母)0ならば,\ 分母をはらっても同値である. 平方完成によって(分母)0を確認して分母をはらい,\ 整理するとxの方程式となる. 2次方程式の実数解条件はD0だが,\ y=1のときは2次方程式にならないので場合分けする. 実際に計算してみることで,\ 実数解をもつことが確認できる. は,\ 前提であるy1との共通範囲にしなければならない. のy=1との12 y<1,\ 10の変形は注意が必要である. つまり,\ 安易に\ 不等式は,\ 両辺に負数を掛けると不等号の向きが逆になるからである. y-1>0\ (y>1)のとき,\ 両辺にy-1を掛けてy<0となるが,\ y>1との共通範囲はない. 同様に,\ {y}{y-1}0の両辺に(y-1)²を掛けると y(y-1)0 よって,\ y0,\ 1 yとなるが,\ y1が前提なのでy0,\ となる.

