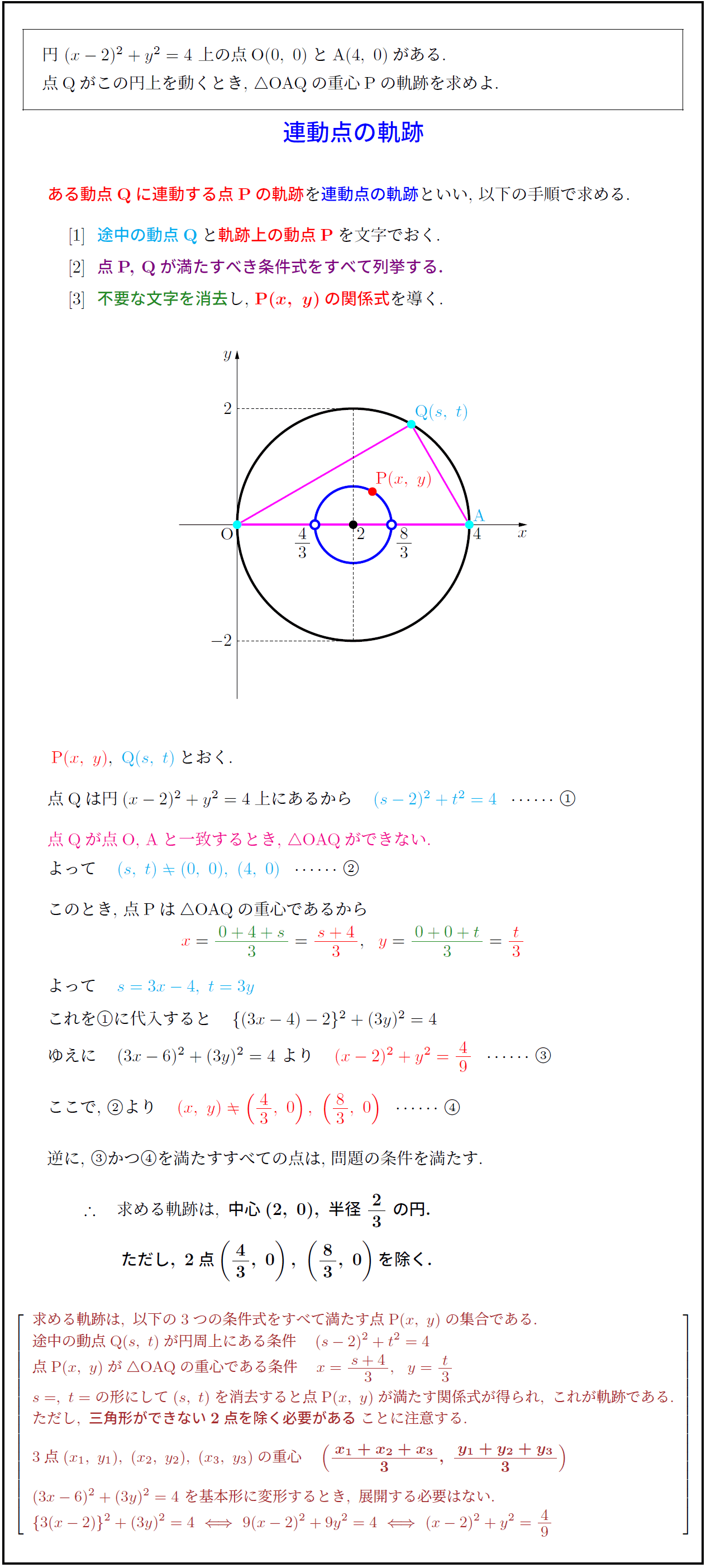
円\ $(x-2)^2+y^2=4\ 上の点O(0,\ 0)とA(4,\ 0)}がある.$
点Q}がこの円上を動くとき,\ $△$OAQ}の重心P}の軌跡を求めよ. 連動点の軌跡}ある動点Qに連動する点Pの軌跡を連動点の軌跡といい,\ 以下の手順で求める.
$[1]$\ \ 途中の動点Qと軌跡上の動点Pを文字でおく.
$[2]$\ \ 点P,\ Qが満たすべき条件式をすべて列挙する.
$[3]$\ \ 不要な文字を消去し,\ P$(x,\ y)}$の関係式を導く点Qが点O,\ Aと一致するとき,\ $△$OAQができない.}
逆に,\ ③かつ④を満たすすべての点は,\ 問題の条件を満たす.
∴ 求める軌跡は,\ 中心(2,\ 0),\ 半径\ 23\ の円.}
求める軌跡は,\ 以下の3つの条件式をすべて満たす点P}(x,\ y)の集合である.
途中の動点Q}(s,\ t)が円周上にある条件 (s-2)^2+t^2=4
点P}(x,\ y)が△OAQ}の重心である条件 x=s+4}{3},\ \ y= t3
s=,\ t=の形にして(s,\ t)を消去すると点 P(x,\ y)が満たす関係式が得られ,\ これが軌跡である.
ただし,\ 三角形ができない2点を除く必要がある}ことに注意する.
(3x-6)^2+(3y)^2=4\ を基本形に変形するとき,\ 展開する必要はない. \

