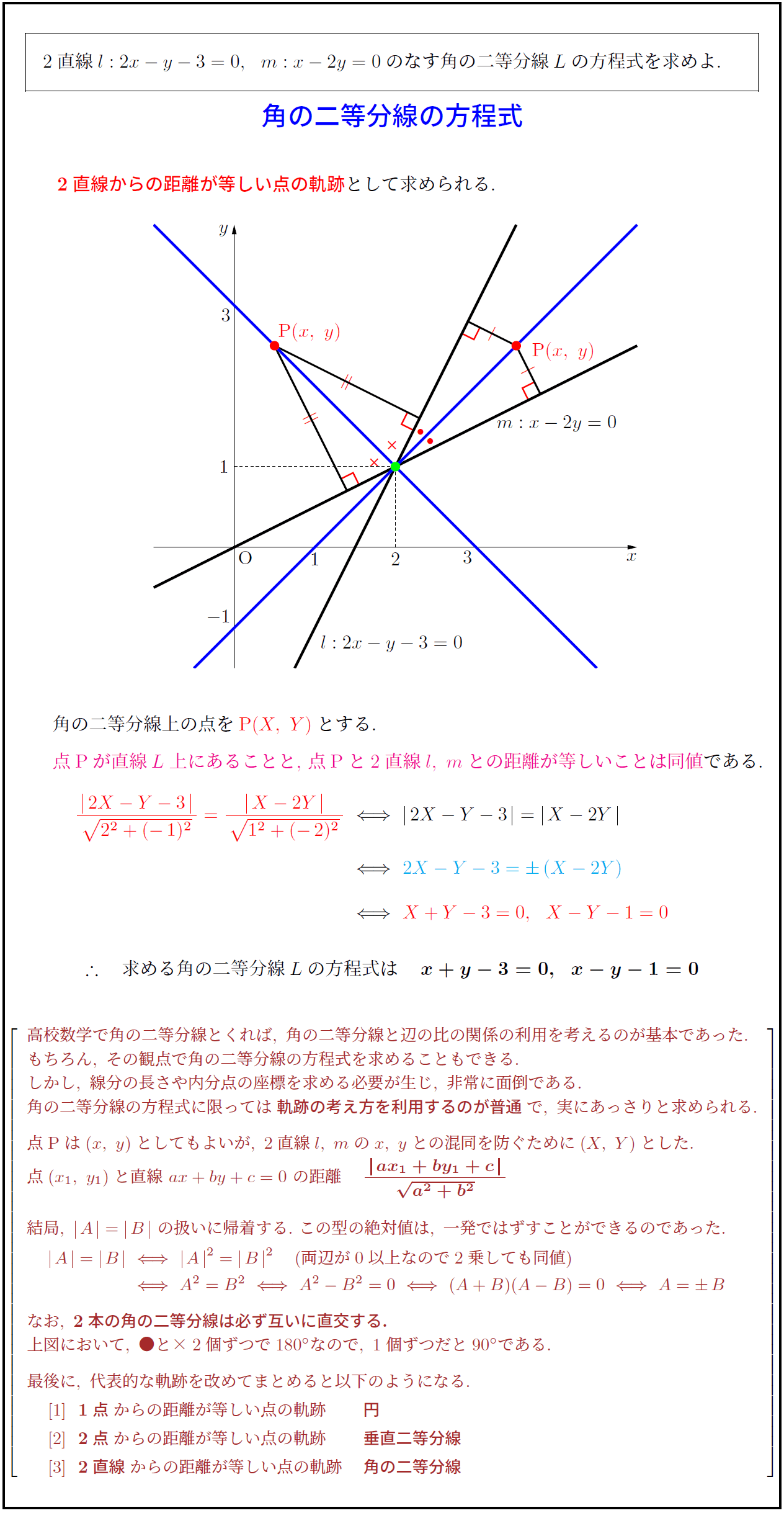
2直線$l:2x-y-3=0,\ \ m:x-2y=0$のなす角の二等分線$L$の方程式を求めよ. \\
角の二等分線の方程式 2直線からの距離が等しい点の軌跡として求められる.
角の二等分線上の点をP$(X,\ Y)$}とする.
点Pが直線$L$上にあることと,\ 点Pと2直線$l,\ m$との距離が等しいことは同値}である. \求める角の二等分線Lの方程式は x+y-3=0,\ \ x-y-1=0}$} \\
$\left[l}
高校数学で角の二等分線とくれば,\ 角の二等分線と辺の比の関係の利用を考えるのが基本であった.
もちろん,\ その観点で角の二等分線の方程式を求めることもできる.
しかし,\ 線分の長さや内分点の座標を求める必要が生じ,\ 非常に面倒である.
角の二等分線の方程式に限っては軌跡の考え方を利用するのが普通}で,\ 実にあっさりと求められる.
点 Pは(x,\ y)としてもよいが,\ 2直線l,\ mのx,\ yとの混同を防ぐために(X,\ Y)とした.
点(x_1,\ y_1)と直線\ ax+by+c=0\ の距離 ax_1+by_1+c{√{a^2+b^2
結局,\ A}=B}\ の扱いに帰着する.\ この型の絶対値は,\ 一発ではずすことができるのであった. \(両辺が0以上なので2乗しても同値) A^2=B^2\ ⇔\ A^2-B^2=0\ ⇔\ (A+B)(A-B)=0\ ⇔\ A=±\,B
なお,\ 2本の角の二等分線は必ず互いに直交する.}
上図において,\ ●と×2個ずつで180° なので,\ 1個ずつだと90° である.
最後に,\ 代表的な軌跡を改めてまとめると以下のようになる.
[1]\ \ 1点}からの距離が等しい点の軌跡 円}
[2]\ \ 2点}からの距離が等しい点の軌跡 垂直二等分線}
[3]\ \ 2直線}からの距離が等しい点の軌跡 角の二等分線}

