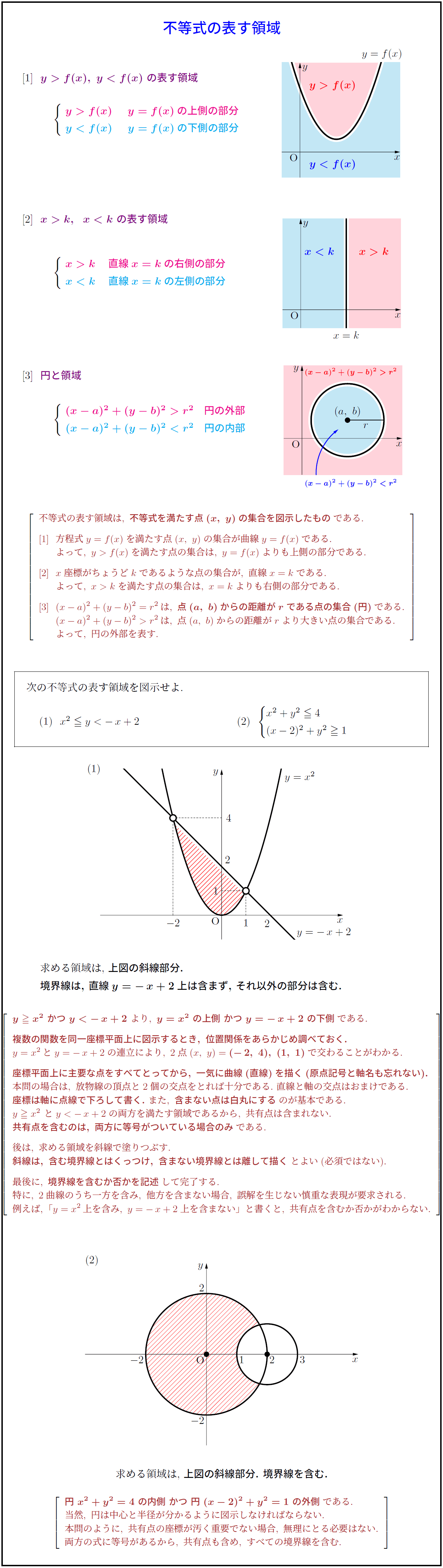
不等式の表す領域は,\ 不等式を満たす点(x,\ y)の集合を図示したもの}である.
[1]}\ \ 方程式y=f(x)を満たす点(x,\ y)の集合が曲線y=f(x)である.
\ \ よって,\ f(x)を満たす点の集合は,\ y=f(x)よりも上側の部分である.
[2]}\ \ x座標がちょうどkであるような点の集合が,\ 直線x=kである.
\ \ よって,\ を満たす点の集合は,\ x=kよりも右側の部分である.
[3]}\ \ (x-a)^2+(y-b)^2=r^2\,は,\ 点(a,\ b)からの距離がrである点の集合(円)}である.
は,\ 点(a,\ b)からの距離がrより大きい点の集合である.
\ \ よって,\ 円の外部を表す.
求める領域は,\ 上図の斜線部分.}
境界線は,\ 直線$y=-\,x+2}$上は含まず,\ それ以外の部分は含む.} \\
複数の関数を同一座標平面上に図示するとき,\ 位置関係をあらかじめ調べておく.}
y=x^2\,とy=-\,x+2の連立により,\ 2点(x,\ y)=(-\,2,\ 4),\ (1,\ 1)}で交わることがわかる.
座標平面上に主要な点をすべてとってから,\ 一気に曲線(直線)を描く(原点記号と軸名も忘れない).}
本問の場合は,\ 放物線の頂点と2個の交点をとれば十分である.\ 直線と軸の交点はおまけである.
座標は軸に点線で下ろして書く.}\ また,\ 含まない点は白丸にする}のが基本である.
y≧ x^2\ とy<-\,x+2の両方を満たす領域であるから,\ 共有点は含まれない.
共有点を含むのは,\ 両方に等号がついている場合のみ}である.
後は,\ 求める領域を斜線で塗りつぶす.
斜線は,\ 含む境界線とはくっつけ,\ 含まない境界線とは離して描く}とよい(必須ではない).
最後に,\ 境界線を含むか否かを記述}して完了する.
特に,\ 2曲線のうち一方を含み,\ 他方を含まない場合,\ 誤解を生じない慎重な表現が要求される.
例えば,\ 「y=x^2\,上を含み,\ y=-\,x+2上を含まない」と書くと,\ 共有点を含むか否かがわからない.
円\ x^2+y^2=4\ の内側\ かつ\ 円\ (x-2)^2+y^2=1\ の外側}である.
当然,\ 円は中心と半径が分かるように図示しなければならない.
本問のように,\ 共有点の座標が汚く重要でない場合,\ 無理にとる必要はない.
両方の式に等号があるから,\ 共有点も含め,\ すべての境界線を含む.

