本問は、根本的な考え方・解の存在範囲(配置)問題(高難度)・領域図示と多くの重要ポイントを含む良問であるが、その分難易度が高い。
特に、解の存在範囲問題の扱いに関しては、すでに基本ができている学生を対象とした簡潔な解説となっている。「2次方程式が少なくとも1つの実数解をもつ条件」については以下で確認してほしい。
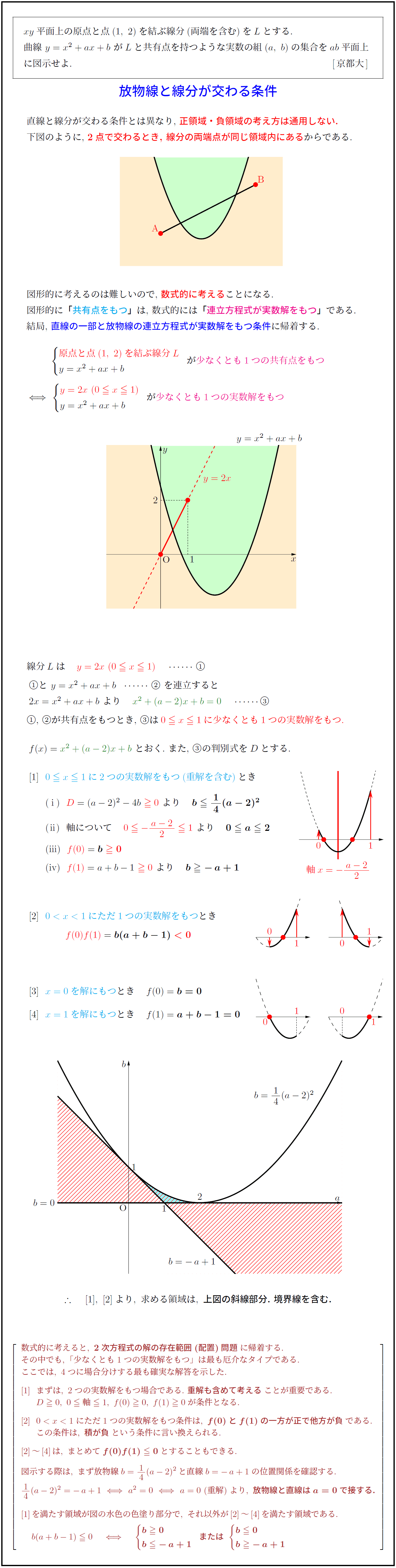
xy平面上の原点と点(1,\ 2)を結ぶ線分(両端を含む)をLとする.$
$曲線\ y=x^2+ax+b\ がLと共有点を持つような実数の組(a,\ b)の集合をab平面上$
$に図示せよ. \ [\,京都大\,]$ 放物線と線分が交わる条件
直線と線分が交わる条件とは異なり,\ 正領域・負領域の考え方は通用しない.
下図のように,\ 2点で交わるとき,\ 線分の両端点が同じ領域内にあるからである.
図形的に考えるのは難しいので,\ 数式的に考えることになる.
図形的に「共有点をもつ}」}は,\ 数式的には「連立方程式が実数解をもつ}」}である.
結局,\ 直線の一部と放物線の連立方程式が実数解をもつ条件に帰着する.
原点と点(1,\ 2)を結ぶ線分L
少なくとも1つの共有点をもつ}$求める領域は,\ 上図の斜線部分.\ 境界線を含む.}$}
数式的に考えると,\ 2次方程式の解の存在範囲(配置)問題}に帰着する.
その中でも,\ 「少なくとも1つの実数解をもつ」は最も厄介なタイプである.
ここでは,\ 4つに場合分けする最も確実な解答を示した.
[1]\ \ まずは,\ 2つの実数解をもつ場合である.\ 重解も含めて考える}ことが重要である.
\ \ D≧0,\ 0≦ 軸≦1,\ f(0)≧0,\ f(1)≧0が条件となる.
ただ1つの実数解をもつ条件は,\ f(0)とf(1)の一方が正で他方が負}である.
\ \ この条件は,\ 積が負}という条件に言い換えられる.
[2]\,~\,[4]}\,は,\ まとめてf(0)f(1)≦0}とすることもできる.
図示する際は,\ まず放物線b=14(a-2)^2\,と直線b=-\,a+1の位置関係を確認する.
14(a-2)^2=-\,a+1\ ⇔\ a^2=0\ ⇔\ a=0\ (重解)より,\ 放物線と直線はa=0で接する.}
[1]}\,を満たす領域が図の水色の色塗り部分で,\ それ以外が\,[2]\,~\,[4]\,を満たす領域である.


