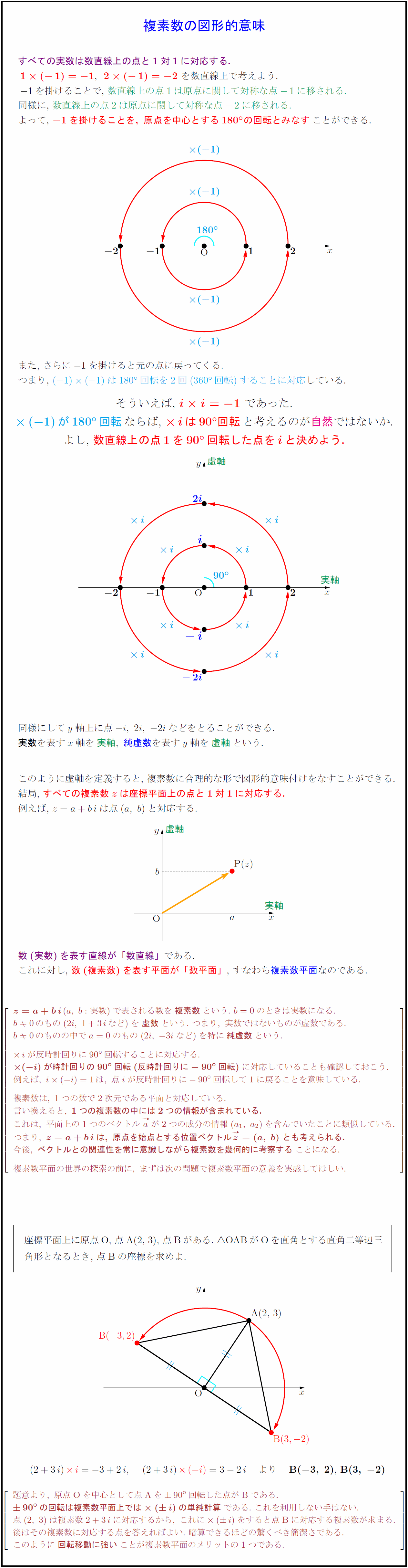
すべての実数は数直線上の点と1対1に対応する. ${1(-1)=-1$,${2(-1)=-2$\ を数直線上で考えよう. $-1$を掛けることで,\ 数直線上の点1は原点に関して対称な点$-1$に移される.} 同様に,\ 数直線上の点2は原点に関して対称な点$-2$に移される.} よって,\ ${-1を掛けることを,\ 原点を中心とする180° の回転とみなす$ことができる. つまり,\ $(-1)(-1)は180°回転を2回(360°回転)することに対応}している.$ そういえば,\ ${i i=-1$\ であった. ${(-1)が180°回転$ならば,\ ${iは90° 回転$と考えるのが自然ではないか. よし,\ 数直線上の点1を90${°}$回転した点を${i}$と決めよう. 同様にして$y$軸上に点$-i,\ 2i,\ -2i$などをとることができる. 実数}を表す$x軸を{実軸,\ 純虚数を表すy軸を{虚軸という.$ このように虚軸を定義すると,\ 複素数に合理的な形で図形的意味付けをなすことができる. 結局,\ すべての複素数${z}$は座標平面上の点と1対1に対応する. 例えば,\ $z={a}+{b}$は点$(a,\ b)$と対応する. 数(実数)を表す直線が「数直線」である. これに対し,\ 数(複素数)を表す平面が「数平面」,\ すなわち複素数平面なのである. $[l} {z={a}+{b(a,\ b:実数)で表される数を{複素数}という.\ b=0のときは実数になる. b0のもの(2i,\ {1}+{3}など)を{虚数}という.\ つまり,\ 実数ではないものが虚数である. b0のものの中でa=0のもの(2i,\ -3iなど)を特に{純虚数}という. iが反時計回りに90°回転することに対応する. {(-i)が時計回りの90°回転(反時計回りに-90°回転)}に対応していることも確認しておこう. 例えば,\ i(-i)=1は,\ 点iが反時計回りに-90°回転して1に戻ることを意味している. 複素数は,\ 1つの数で2次元である平面と対応している. 言い換えると,\ {1つの複素数の中には2つの情報が含まれている.} これは,\ 平面上の1つのベクトル aが2つの成分の情報(a₁,\ a₂)を含んでいたことに類似している. つまり,\ {z={a}+{b}は,\ 原点を始点とする位置ベクトル z=(a,\ b)\ とも考えられる.} 今後,\ {ベクトルとの関連性を常に意識しながら複素数を幾何的に考察する}ことになる. 複素数平面の世界の探索の前に,\ まずは次の問題で複素数平面の意義を実感してほしい. }]$ |} [-.8zh] 座標平面上に原点O,\ 点A(2,\ 3),\ 点Bがある.\ $$OABがOを直角とする直角二等辺三 角形となるとき,\ 点Bの座標を求めよ. [-.8zh] 題意より,\ 原点{O}を中心として点{A}を90°回転した点がB}である. {90°の回転は複素数平面上では (i)の単純計算}である.\ これを利用しない手はない. 点(2,\ 3)は複素数{2}+{3}に対応するから,\ これに(i)をすると点B}に対応する複素数が求まる. 後はその複素数に対応する点を答えればよい.\ 暗算できるほどの驚くべき簡潔さである. このように{回転移動に強い}ことが複素数平面のメリットの1つである.

