本項目は極限分野の知識を要します。
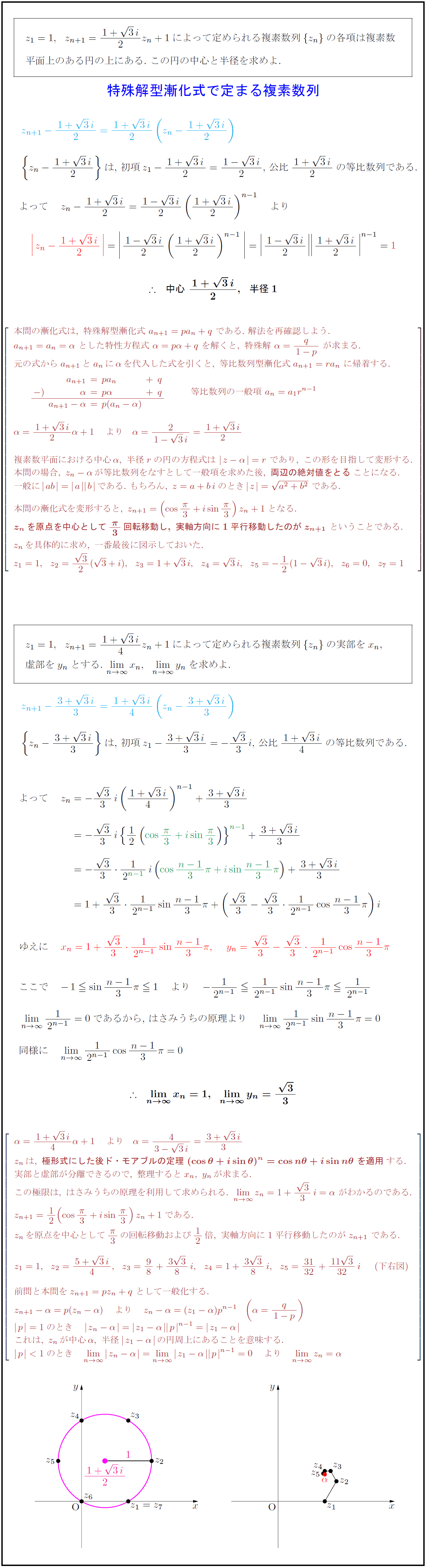
z₁=1,z_{n+1}={1+3i}{2}z_n+1$によって定められる複素数列${z_n}$の各項は複素数 平面上のある円の上にある.\ この円の中心と半径を求めよ. 特殊解型漸化式で定まる複素数列 本問の漸化式は,\ 特殊解型漸化式\ a_{n+1}=pa_n+q\ である.\ 解法を再確認しよう. a_{n+1}=a_n=α\ とした特性方程式\ α=pα+q\ を解くと,\ 特殊解\ α={q}{1-p}\ が求まる. 元の式からa_{n+1}とa_nにαを代入した式を引くと,\ 等比数列型漸化式a_{n+1}=ra_n\ に帰着する. 等比数列の一般項\ a_n=a₁r^{n-1} 複素数平面における中心α,\ 半径rの円の方程式は\ z-α}=r\ であり,\ この形を目指して変形する. 本問の場合,\ z_n-αが等比数列をなすとして一般項を求めた後,\ {両辺の絶対値をとる}ことになる. 一般にab}= a bである.\ もちろん,\ z=a+biのとき|z|={a²+b²}\ である. 本問の漸化式を変形すると,\ z_{n+1}=(π}{3)z_n+1となる. {z_nを原点を中心として{π}{3}回転移動し,\ 実軸方向に1平行移動したのがz_{n+1\ ということである. z_nを具体的に求め,\ 一番最後に図示しておいた. z₁=1,z_{n+1}={1+3i}{4}z_n+1$によって定められる複素数列${z_n}$の実部を$x_n$,\ 虚部を$y_n$とする.\ $lim[n→∞]x_n,lim[n→∞]y_n$を求めよ. 4}$の等比数列である. $lim[n→∞]{1}{2^{n-1=0$であるから,\ はさみうちの原理より z_nは,\ {極形式にした後ド・モアブルの定理\ ({θ})^n={nθ}\ を適用}する. 実部と虚部が分離できるので,\ 整理するとx_n,\ y_nが求まる. この極限は,\ はさみうちの原理を利用して求められる.\ lim[n→∞]z_n=1+{3}{3}i=α\ がわかるのである. z_nを原点を中心として{π}{3}の回転移動および12倍,\ 実軸方向に1平行移動したのがz_{n+1}\ である. 前問と本問をz_{n+1}=pz_n+q\ として一般化する. これは,\ z_nが中心α,\ 半径z₁-α}の円周上にあることを意味する.

