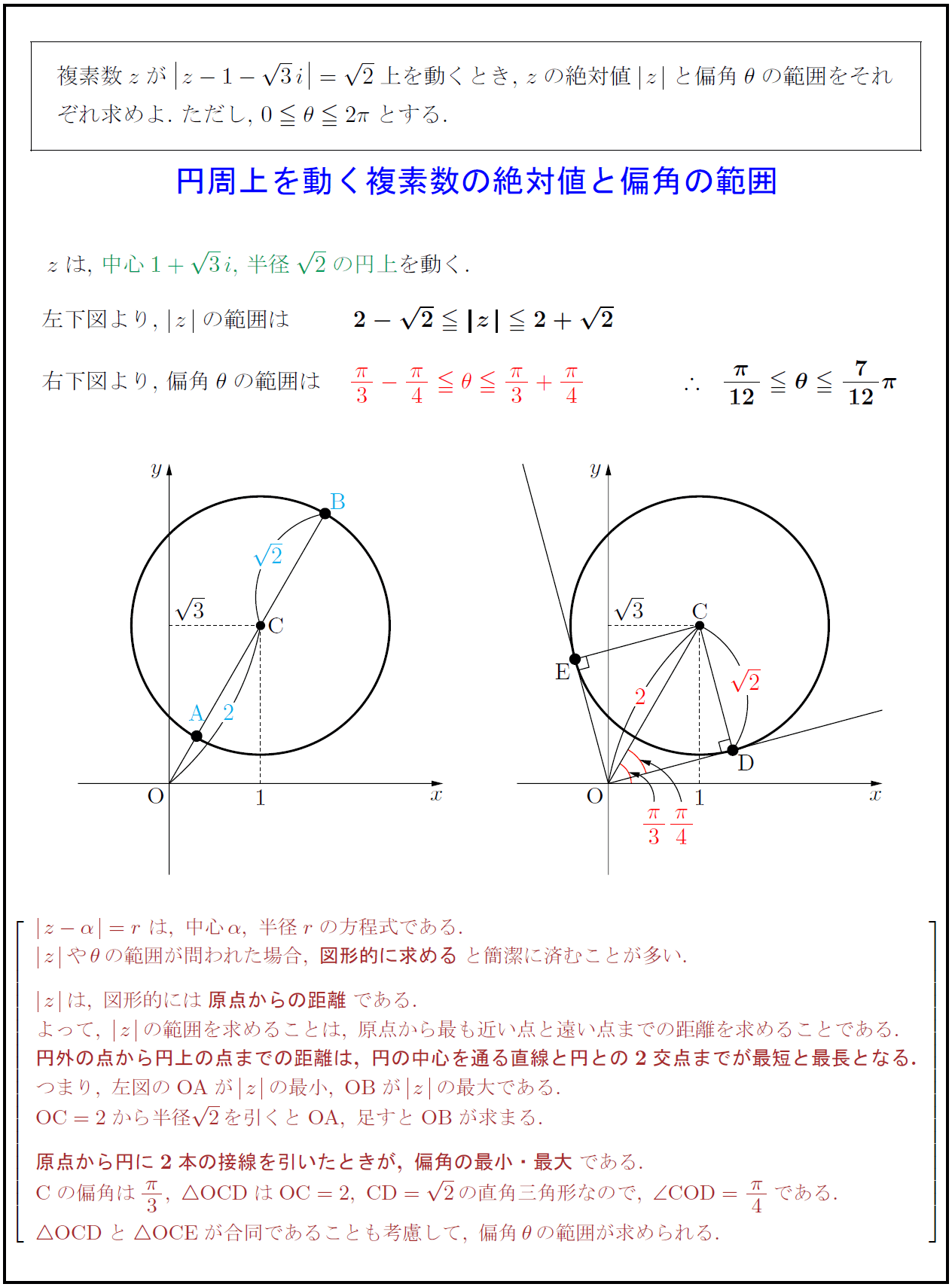
複素数$z$が$z-1-3i}=2$上を動くとき,\ $z$の絶対値$|z|$と偏角$θ$の範囲をそれ 円周上を動く複素数の絶対値と偏角の範囲 $z$は, {中心$1+3i$,\ 半径$2$の円上}を動く. 左下図より,\ $|z|$の範囲は 右下図より,\ 偏角$θ$の範囲は z-α}=r\ は,\ 中心α,\ 半径rの方程式である. |z|やθの範囲が問われた場合,\ {図形的に求める}と簡潔に済むことが多い. |z|は,\ 図形的には{原点からの距離}である. よって,\ |z|の範囲を求めることは,\ 原点から最も近い点と遠い点までの距離を求めることである. {円外の点から円上の点までの距離は,\ 円の中心を通る直線と円との2交点までが最短と最長となる.} {つまり,\ 左図のOAが|z|の最小,\ OBが|z|の最大である.} {OC=2}から半径2を引くと{OA},\ 足すと{OB}が求まる. {原点から円に2本の接線を引いたときが,\ 偏角の最小・最大}である. {Cの偏角は{π}{3},\ OCDはOC=2,\ CD=2}の直角三角形なので,\ {∠ COD={π}{4である. { OCDと OCE}が合同であることも考慮して,\ 偏角θの範囲が求められる.

