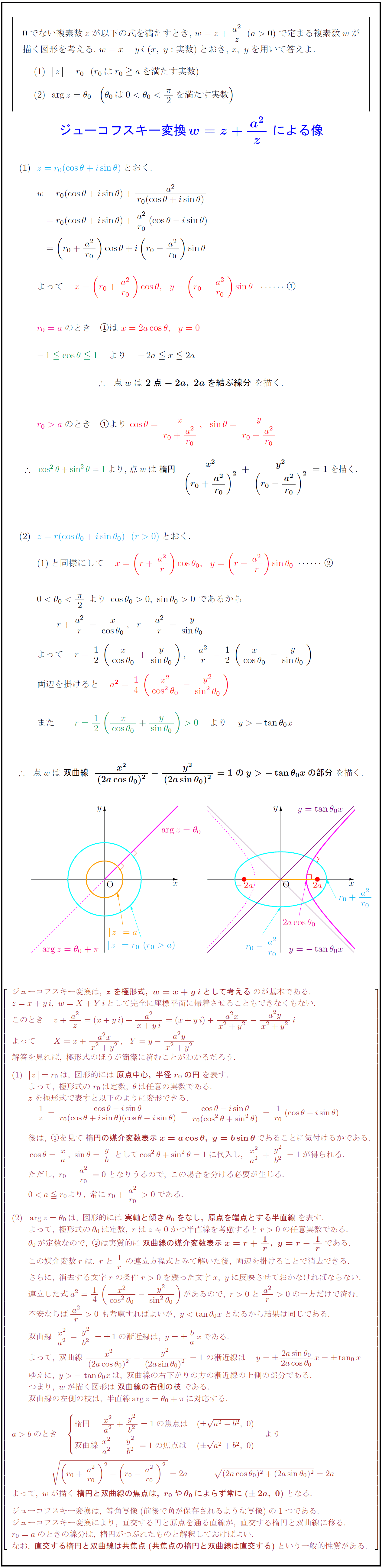
0でない複素数$z$が以下の式を満たすとき,\ $w=z+{a²}{z}\ (a>0)$で定まる複素数$w$が 描く図形を考える.\ $w=x+yi\ (x,\ y:実数)$とおき,\ $x,\ y$を用いて答えよ. $|z|=r₀(r₀はr₀ aを満たす実数)$ {ジューコフスキー変換w=z+{a²}{z}\ による像}$ ジューコフスキー変換は,\ {zを極形式,\ w=x+yiとして考える}のが基本である. z=x+yi,\ w=X+Yiとして完全に座標平面に帰着させることもできなくもない. このとき z+{a²}{z}=(x+yi)+{a²}{x+yi}=(x+yi)+{a²x}{x²+y²}-{a²y}{x²+y²}i よって X=x+{a²x}{x²+y²},Y=y-{a²y}{x²+y²} 解答を見れば,\ 極形式のほうが簡潔に済むことがわかるだろう. z}=r₀は,\ 図形的には{原点中心,\ 半径r₀の円}を表す. よって,\ 極形式のr₀は定数,\ θは任意の実数である. zを極形式で表すと以下のように変形できる. 後は,\ を見て{楕円の媒介変数表示x=acosθ,\ y=bsinθ}であることに気付けるかである. ただし,\ r₀-{a²}{r₀}=0となりうるので,\ この場合を分ける必要が生じる. \ arg z=θ₀は,\ 図形的には{実軸と傾きθ₀をなし,\ 原点を端点とする半直線}を表す. よって,\ 極形式のθ₀は定数,\ rはz0かつ半直線を考慮するとr>0の任意実数である. θ₀が定数なので,\ は実質的に{双曲線の媒介変数表示x=r+1r,\ y=r-1r}である. この媒介変数rは,\ rと1rの連立方程式とみて解いた後,\ 両辺を掛けることで消去できる. さらに,\ 消去する文字rの条件r>0を残った文字x,\ yに反映させておかなければならない. 連立した式a²=14({x²}{cos²θ₀}-{y²}{sin²θ₀})があるので,\ r>0と{a²}{r}>0の一方だけで済む. 不安ならば{a²}{r}>0\ も考慮すればよいが,\ y-tanθ₀xは,\ 双曲線の右下がりの方の漸近線の上側の部分である. つまり,\ wが描く図形は{双曲線の右側の枝}である. 双曲線の左側の枝は,\ 半直線arg z=θ₀+πに対応する. 楕円 \ {x²}{a²}+{y²}{b²}=1の焦点は & ({a²-b²},\ 0) 双曲線{x²}{a²}-{y²}{b²}=1の焦点は & ({a²+b²},\ 0) よって,\ wが描く{楕円と双曲線の焦点は,\ r₀やθ₀によらず常に(2a,\ 0)}となる. ジューコフスキー変換は,\ 等角写像(前後で角が保存されるような写像)の1つである. ジューコフスキー変換により,\ 直交する円と原点を通る直線が,\ 直交する楕円と双曲線に移る. r₀=aのときの線分は,\ 楕円がつぶれたものと解釈しておけばよい. なお,\ {直交する楕円と双曲線は共焦点(共焦点の楕円と双曲線は直交する)}という一般的性質がある.

