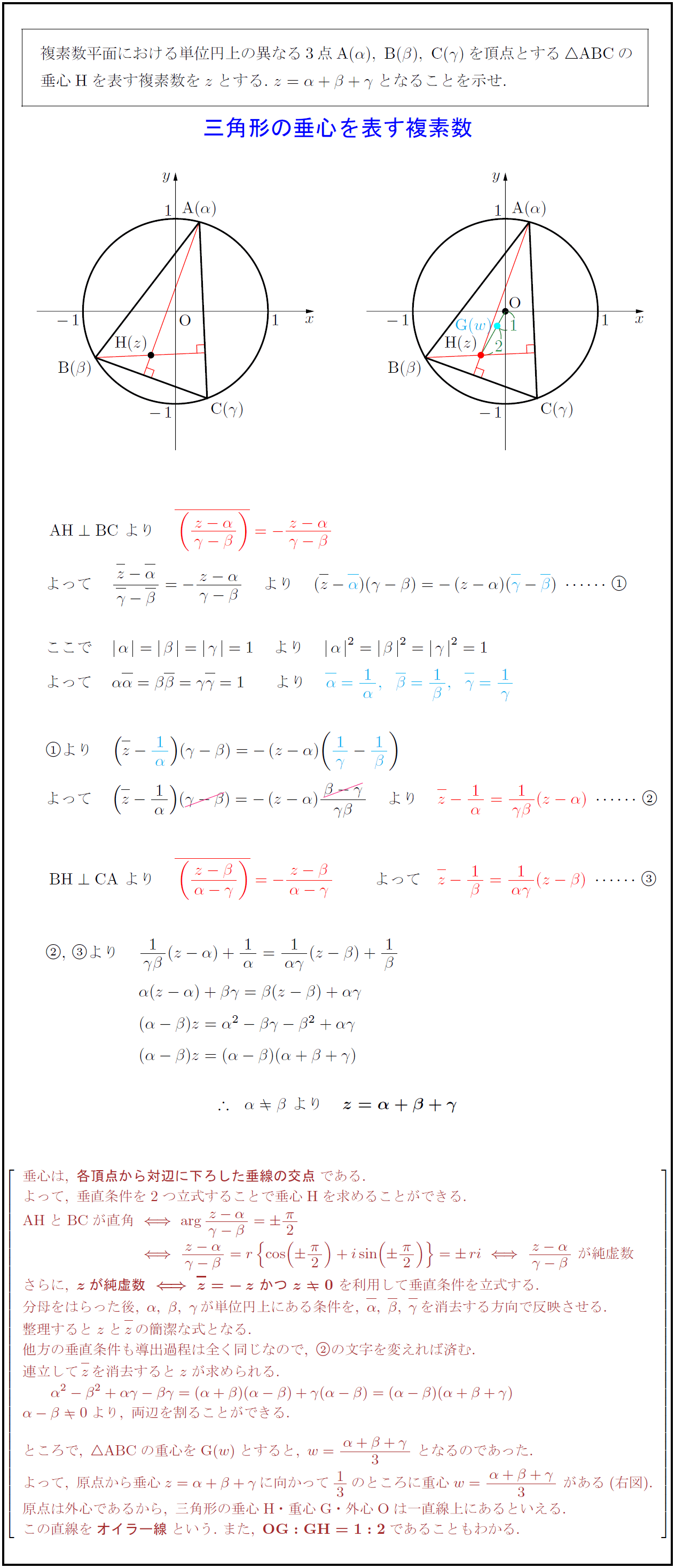
複素数平面における単位円上の異なる3点${A(α),\ B(β),\ C(γ)}$を頂点とする$$ABCの 垂心Hを表す複素数を$z$とする.\ $z=α+β+γ$となることを示せ. {三角形の垂心を表す複素数 垂心は,\ {各頂点から対辺に下ろした垂線の交点}である. よって,\ 垂直条件を2つ立式することで垂心 Hを求めることができる. {AHとBC}が直角] AHとBC}が直角}\ }\ が純虚数 さらに,\ {zが純虚数 z=-z\ かつ\ z0}\ を利用して垂直条件を立式する. 分母をはらった後,\ α,\ β,\ γが単位円上にある条件を,\ α,\ β,\ γを消去する方向で反映させる. 整理するとzと zの簡潔な式となる. 他方の垂直条件も導出過程は全く同じなので,\ の文字を変えれば済む. 連立して zを消去するとzが求められる. α-β0より,\ 両辺を割ることができる. ところで,\ ABC}の重心を G(w)とすると,\ w={α+β+γ}{3}\ となるのであった. よって,\ 原点から垂心z=α+β+γに向かって13のところに重心w={α+β+γ}{3}\ がある(右図). 原点は外心であるから,\ 三角形の垂心 H・重心 G・外心 Oは一直線上にあるといえる. この直線を{オイラー線}という.\ また,\ OG:GH}=1:2}であることもわかる.

