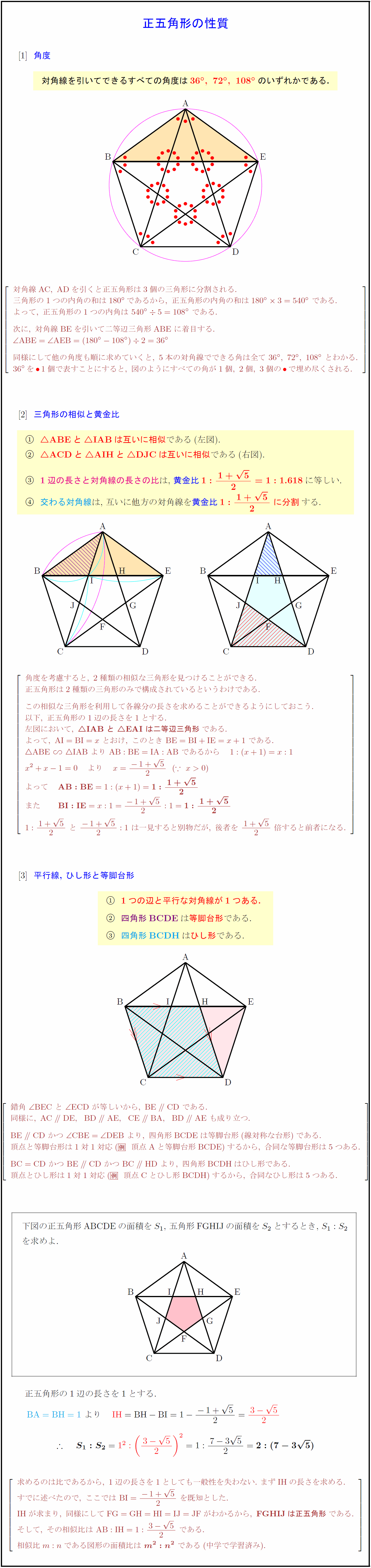
角度 dy}{l} 対角線を引いてできるすべての角度は${36°,\ 72°,\ 108°$のいずれかである.} 対角線{AC,\ AD}を引くと正五角形は3個の三角形に分割される. 三角形の1つの内角の和は180°であるから,\ 正五角形の内角の和は180°3=540°\ である. よって,\ 正五角形の1つの内角は\ 540° 5=108°\ である. 次に,\ 対角線{BEを引いて二等辺三角形ABE}\ に着目する. {∠ ABE=∠ AEB=(180°-108°)2}=36° 同様にして他の角度も順に求めていくと,\ 5本の対角線でできる角は全て\ 36°,\ 72°,\ 108°\ とわかる. 36°を\bullet}1個で表すことにすると,\ 図のようにすべての角が1個,\ 2個,\ 3個の\bullet}で埋め尽くされる.{三角形の相似と黄金比IABは互いに相似である(左図). $$ACDと$$AIHと$$DJCは互いに相似である(右図). 1辺の長さと対角線の長さの比は,\ 黄金比${1:{1+5}{2}=1:1.618$に等しい. 交わる対角線は,\ 互いに他方の対角線を黄金比${1:{1+5}{2}\ に分割$する. 角度を考慮すると,\ 2種類の相似な三角形を見つけることができる. 正五角形は2種類の三角形のみで構成されているというわけである. この相似な三角形を利用して各線分の長さを求めることができるようにしておこう. 以下,\ 正五角形の1辺の長さを1とする. 左図において,\ IAB\ と\ EAI}\ は二等辺三角形}である. よって,\ {AI=BI=x\ とおけ,\ このとき\ BE=BI+IE=x+1\ である.} は一見すると別物だが,\ 後者を\ {1+5}{2}\ 倍すると前者になる. 平行線,\ ひし形と等脚台形 dy}{l} 1つの辺と平行な対角線が1つある. 四角形BCDEは等脚台形である. 四角形BCDHはひし形である. 錯角\ {∠ BEC\ と\ ∠ ECD\ が等しいから,\ BE∥ CD}\ である. 同様に,\ {AC∥ DE,BD∥ AE,CE∥ BA,BD∥ AE}\ も成り立つ. {BE∥ CD\ かつ\ ∠ CBE=∠ DEB\ より,\ 四角形BCDE}は等脚台形(線対称な台形)である. {頂点と等脚台形は1対1対応(頂点Aと等脚台形BCDE)するから,\ 合同な等脚台形は5つある.} {BC=CD\ かつ\ BE∥ CD\ かつ\ BC∥ HD\ より,\ 四角形BCDHはひし形である.} {頂点とひし形は1対1対応(頂点Cとひし形BCDH)するから,\ 合同なひし形は5つある.} 下図の正五角形ABCDEの面積を$S₁$,\ 五角形FGHIJの面積を$S₂$とするとき,\ $S₁:S₂$ 正五角形の1辺の長さを1とする. 求めるのは比であるから,\ 1辺の長さを1としても一般性を失わない.\ まず{IH}の長さを求める. すでに述べたので,\ ここでは\ {BI={-1+5}{2\ を既知とした. {IHが求まり,\ 同様にしてFG=GH=HI=IJ=JFがわかるから,\ {FGHIJは正五角形}である.} そして,\ その相似比は\ {AB:IH=1:{3-5}{2\ である. 相似比m:nである図形の面積比は\ {m²:n²}\ である(中学で学習済み).

