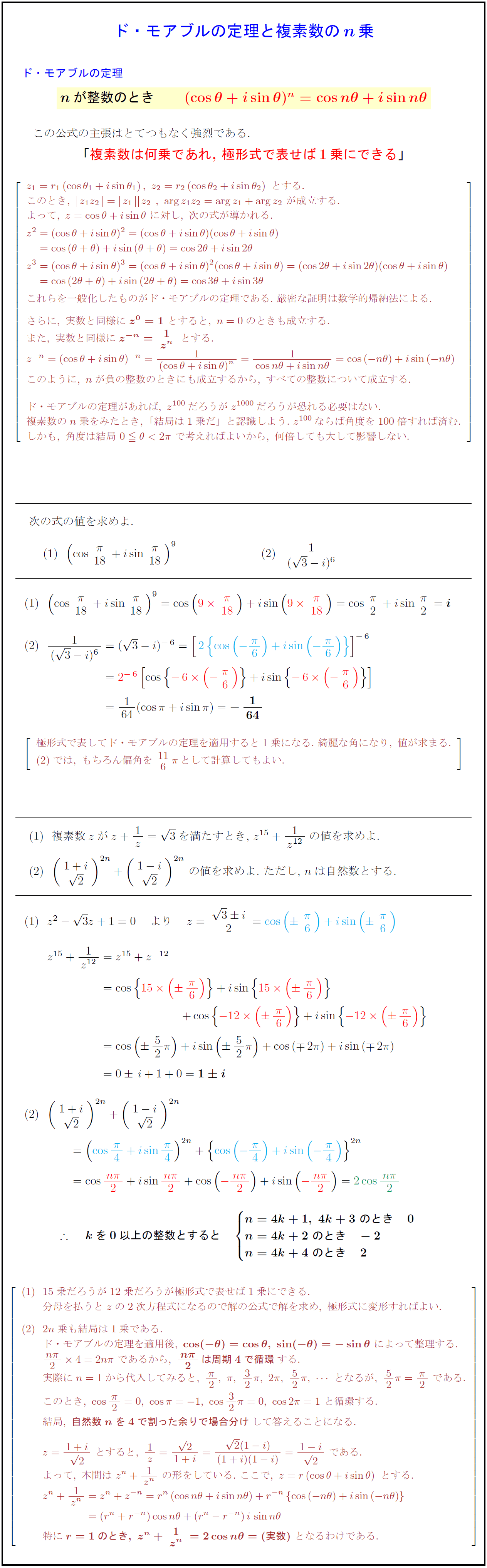
この公式の主張はとてつもなく強烈である. 「複素数は何乗であれ,\ 極形式で表せば1乗にできる}」} よって,\ z={θ}\ に対し,\ 次の式が導かれる. これらを一般化したものがド・モアブルの定理である.\ 厳密な証明は数学的帰納法による. さらに,\ 実数と同様に{z^0=1}\ とすると,\ n=0のときも成立する. このように,\ nが負の整数のときにも成立するから,\ すべての整数について成立する. ド・モアブルの定理があれば,\ z^{100}だろうがz^{1000}だろうが恐れる必要はない. 複素数のn乗をみたとき,\ 「結局は1乗だ」と認識しよう.\ z^{100}ならば角度を100倍すれば済む. しかも,\ 角度は結局\ 0θ<2π\ で考えればよいから,\ 何倍しても大して影響しない. $[l} 極形式で表してド・モアブルの定理を適用すると1乗になる.\ 綺麗な角になり,\ 値が求まる. では,\ もちろん偏角を{11}{6}πとして計算してもよい. 15乗だろうが12乗だろうが極形式で表せば1乗にできる. 分母を払うとzの2次方程式になるので解の公式で解を求め,\ 極形式に変形すればよい. 2n乗も結局は1乗である. ド・モアブルの定理を適用後,\ {cos(-θ)=cosθ,\ sin(-θ)=-sinθ}\ によって整理する. {nπ}{2}4=2nπ\ であるから,\ nπ}{2}は周期4で循環}する. 実際にn=1から代入してみると,\ {π}{2},\ π,\ 32π,\ 2π,\ 52π,となるが,\ 52π={π}{2}\ である. このとき,\ cos{π}{2}=0,\ cosπ=-1,\ cos32π=0,\ cos2π=1\ と循環する. 結局,\ {自然数nを4で割った余りで場合分け}して答えることになる. z^n+{1}{z^n}=z^n+z^{-n}=[r^n]{nθ}+[r^{-n}][{]{(-nθ)} {z^n+{1}{z^n=(r^n+r^{-n})cos nθ+(r^n-r^{-n})sin nθ 特に{r=1のとき,\ z^n+{1}{z^n}=2cos nθ=(実数)}\ となるわけである.

