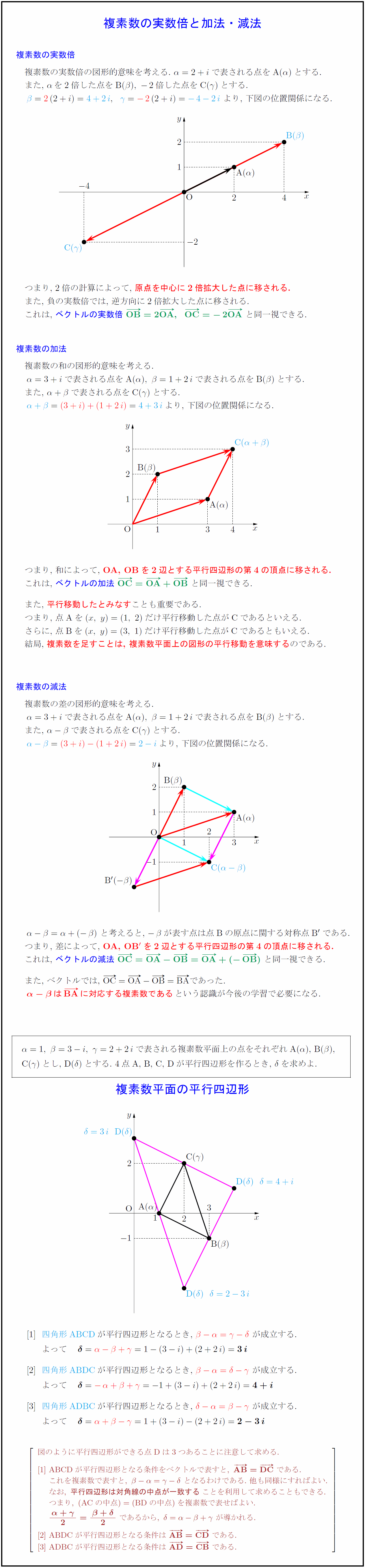
複素数の実数倍の図形的意味を考える.\ $α={2}+{1}$で表される点をA($α$)とする. また,\ $αを2倍した点をB}(β),\ -2倍した点をC}(γ)とする.$ $β}=2}({2}+{1})={4}+{2,γ}=-2}({2}+{1})=-{4}-{2$\ より,\ 下図の位置関係になる. つまり,\ 2倍の計算によって,\ 原点を中心に2倍拡大した点に移される. また,\ 負の実数倍では,\ 逆方向に2倍拡大した点に移される. これは,\ ベクトルの実数倍\ ${OB}=2OA},OC}=-2OA}$}\ と同一視できる. 複素数の加法 複素数の和の図形的意味を考える. $α={3}+{1}で表される点をA}(α),\ β={1}+{2}で表される点をB}(β)とする.$ また,\ $α+β$で表される点をC($γ$)とする. $α+β}=({3}+{1})+({1}+{2})}={4}+{3$より,\ 下図の位置関係になる. つまり,\ 和によって,\ OA,\ OBを2辺とする平行四辺形の第4の頂点に移される. これは,\ ベクトルの加法\ ${OC}=OA}+OB}$}\ と同一視できる. また,\ 平行移動したとみなすことも重要である. つまり,\ 点Aを$(x,\ y)=(1,\ 2)$だけ平行移動した点がCであるといえる. さらに,\ 点Bを$(x,\ y)=(3,\ 1)$だけ平行移動した点がCであるともいえる. 結局,\ 複素数を足すことは,\ 複素数平面上の図形の平行移動を意味するのである. 複素数の減法 複素数の差の図形的意味を考える. $α={3}+{1}で表される点をA}(α),\ β={1}+{2}で表される点をB}(β)とする.$ また,\ $α-β$で表される点をC($γ$)とする. $α-β}=({3}+{1})-({1}+{2})}={2}-{1$より,\ 下図の位置関係になる. $α-β=α+(-β)$\ と考えると,\ $-β$が表す点は点Bの原点に関する対称点B$’$である. つまり,\ 差によって,\ OA,\ OB$’$を2辺とする平行四辺形の第4の頂点に移される. これは,\ ベクトルの減法\ ${OC}=OA}-OB}=OA}+(-OB})$}\ と同一視できる. また,\ ベクトルでは,\ $OC}=OA}-OB}=BA}$}であった. ${α-βはBA}に対応する複素数である$}という認識が今後の学習で必要になる. $α=1,\ β={3}-{1},\ γ={2}+{2}$で表される複素数平面上の点をそれぞれA($α$),\ B($β$), C($γ$)とし,\ D($δ$)とする.\ 4点A,\ B,\ C,\ Dが平行四辺形を作るとき,\ $δ$を求めよ. [-.8zh] { 複素数平面の平行四辺形 四角形ABCD}が平行四辺形となるとき,\ $β-α=γ-δ}$\ が成立する. \ よって ${δ}=α-β+γ}=1-({3}-{1})+({2}+{2})={3i}$ 四角形ABDC}が平行四辺形となるとき,\ $β-α=δ-γ}$\ が成立する. \ よって ${δ}=-α+β+γ}=-1+({3}-{1})+({2}+{2})=4}+{1$ [3]四角形ADBC}が平行四辺形となるとき,\ $δ-α=β-γ}$\ が成立する. \ よって ${δ}=α+β-γ}=1+({3}-{1})-({2}+{2})=2}-{3$ $[l} 図のように平行四辺形ができる点D}は3つあることに注意して求める. \ ABCD}が平行四辺形となる条件をベクトルで表すと,\ {AB}=DC\ である. \ これを複素数で表すと,\ β-α=γ-δ\ となるわけである.\ 他も同様にすればよい. \ なお,\ {平行四辺形は対角線の中点が一致する}ことを利用して求めることもできる. \ つまり,\ (AC}の中点)=(BD}の中点)を複素数で表せばよい. \ α+γ}{2}={β+δ}{2\ であるから,\ δ=α-β+γ\ が導かれる. \ ABDC}が平行四辺形となる条件は\ {AB}=CD\ である. [3]\ ADBC}が平行四辺形となる条件は\ {AD}=CB\ である.

