連立不等式$x^2+y^2≦25,\ x+2y≦10$が表す領域を$D$とする.\ また,\ $a$を実数とする.
点$(x,\ y)$が領域$D$を動くとき,\ $ax+y$の最小値と最大値を求めよ. \\
連立不等式と2変数関数$ax+y}$の最大・最小
基本方針は,\ 前項で説明したとおりである.
ただし,\ 本問は直線の傾きが$-\,a$であり,\ 一定ではない.
よって,\ $a}$の値で場合分けして考える必要が生じる.
$ax+y=k\ とおくと y=-\,ax+k} ・・・・・・\,①$
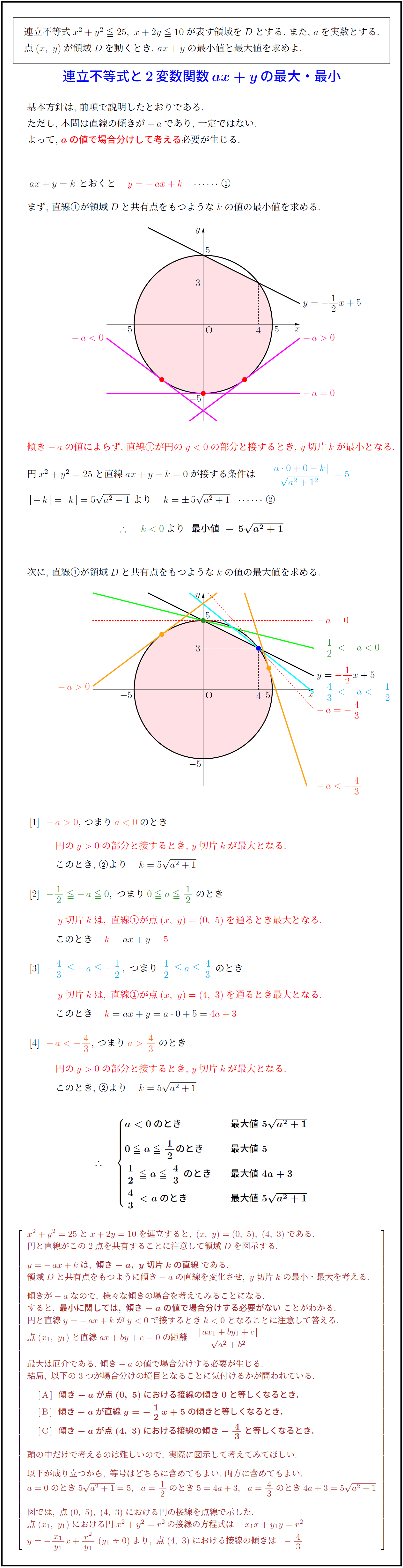
まず,\ 直線①が領域$D$と共有点をもつような$k$の値の最小値を求める.傾き$-\,a$の値によらず,\ 直線①が円のの部分と接するとき,\ $y$切片$k$が最小となる.}
円$x^2+y^2=25$と直線$ax+y-k=0$が接する条件は
次に,\ $直線①が領域Dと共有点をもつようなkの値の最大値を求める.円のの部分と接するとき,\ $y$切片$k$が最大となる.}
[1]}\ \ このとき,\ ②より $k=5√{a^2+1}$
[2]\ \ $-12≦-\,a≦0},\ つまり0≦ a≦12}$のとき
[1]}\ \ $y切片kは,\ 直線①が点(x,\ y)=(0,\ 5)を通るとき最大となる.y切片kは,\ 直線①が点(x,\ y)=(4,\ 3)を通るとき最大となる.{円のの部分と接するとき,\ $y$切片$k$が最大となる.} \\
x^2+y^2=25とx+2y=10を連立すると,\ (x,\ y)=(0,\ 5),\ (4,\ 3)である.
円と直線がこの2点を共有することに注意して領域Dを図示する.
y=-\,ax+kは,\ 傾き-a,\ y切片kの直線}である.
領域Dと共有点をもつように傾き-aの直線を変化させ,\ y切片kの最小・最大を考える.
傾きが-aなので,\ 様々な傾きの場合を考えてみることになる.
すると,\ 最小に関しては,\ 傾き-aの値で場合分けする必要がない}ことがわかる.
円と直線y=-\,ax+kがなることに注意して答える.
点(x_1,\ y_1)と直線ax+by+c=0の距離 ax_1+by_1+c{√{a^2+b^2
最大は厄介である.\ 傾き-aの値で場合分けする必要が生じる.
結局,\ 以下の3つが場合分けの境目となることに気付けるかが問われている.
[\,A}\,]\ \ 傾き-aが点(0,\ 5)における接線の傾き0と等しくなるとき.}
[\,B}\,]\ \ 傾き-aが直線y=-12x+5の傾きと等しくなるとき.}
[\,C}\,]\ \ 傾き-aが点(4,\ 3)における接線の傾き-43\,と等しくなるとき.}
頭の中だけで考えるのは難しいので,\ 実際に図示して考えてみてほしい.
以下が成り立つから,\ 等号はどちらに含めてもよい.\ 両方に含めてもよい.
a=0のとき5√{a^2+1}=5,\ \ a=12\,のとき5=4a+3,\ \ a=43\,のとき4a+3=5√{a^2+1}
図では,\ 点(0,\ 5),\ (4,\ 3)における円の接線を点線で示した.
点(x_1,\ y_1)における円x^2+y^2=r^2\,の接線の方程式は x_1x+y_1y=r^2

