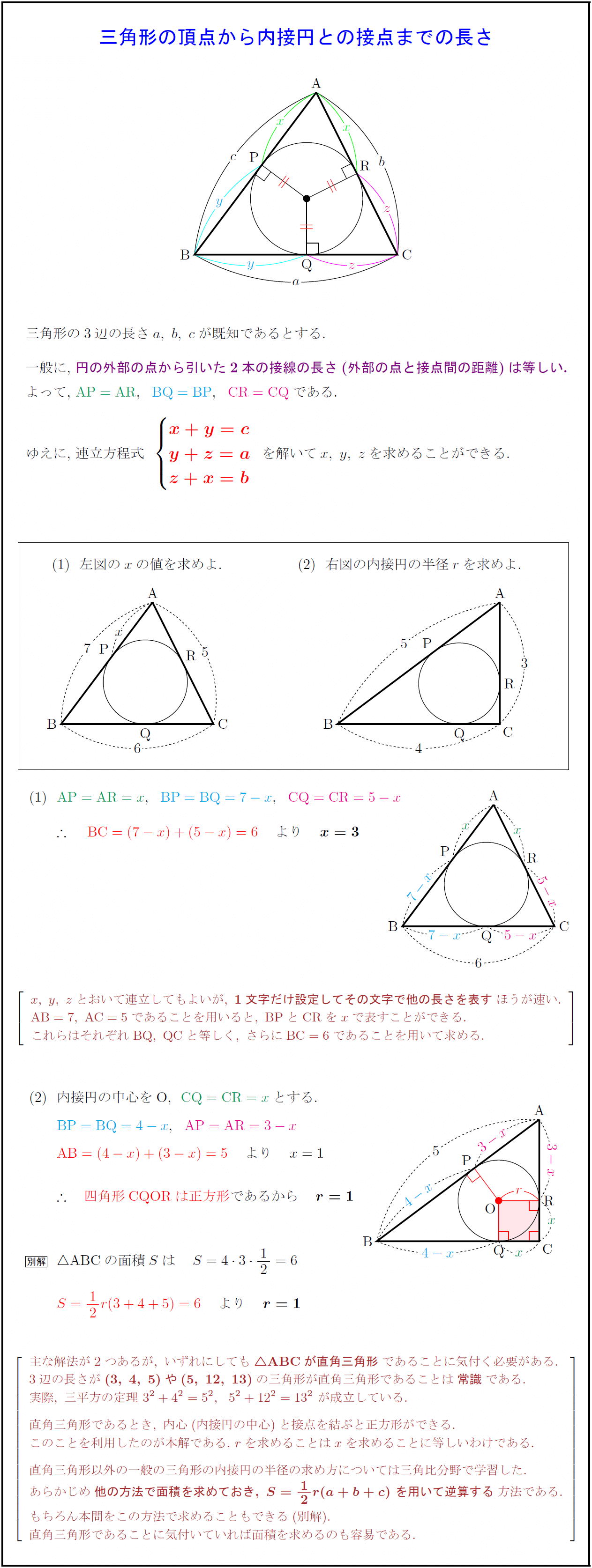
三角形の3辺の長さ$a,\ b,\ c$が既知であるとする. 一般に,\ 円の外部の点から引いた2本の接線の長さ(外部の点と接点間の距離)は等しい. 連立方程式左図の$x$の値を求めよ. 右図の内接円の半径$r$を求めよ. x,\ y,\ zとおいて連立してもよいが,\ {1文字だけ設定してその文字で他の長さを表す}ほうが速い. {AB=7,\ AC=5であることを用いると,\ BPとCRをxで表すことができる.} これらは{それぞれBQ,\ QCと等しく,\ さらにBC=6であることを用いて求める.} 内接円の中心をO,\ 四角形{CQOR}は正方形}であるから 主な解法が2つあるが,\ いずれにしてもABC}が直角三角形}であることに気付く必要がある. 3辺の長さが{(3,\ 4,\ 5)や(5,\ 12,\ 13)}の三角形が直角三角形であることは{常識}である. 実際,\ 三平方の定理\ 3²+4²=5²,5²+12²=13²\ が成立している. 直角三角形であるとき,\ 内心(内接円の中心)と接点を結ぶと正方形ができる. このことを利用したのが本解である.\ rを求めることはxを求めることに等しいわけである. 直角三角形以外の一般の三角形の内接円の半径の求め方については三角比分野で学習した. あらかじめ{他の方法で面積を求めておき,\ S=12r(a+b+c)\ を用いて逆算する}方法である. もちろん本問をこの方法で求めることもできる(別解). 直角三角形であることに気付いていれば面積を求めるのも容易である. }]$

