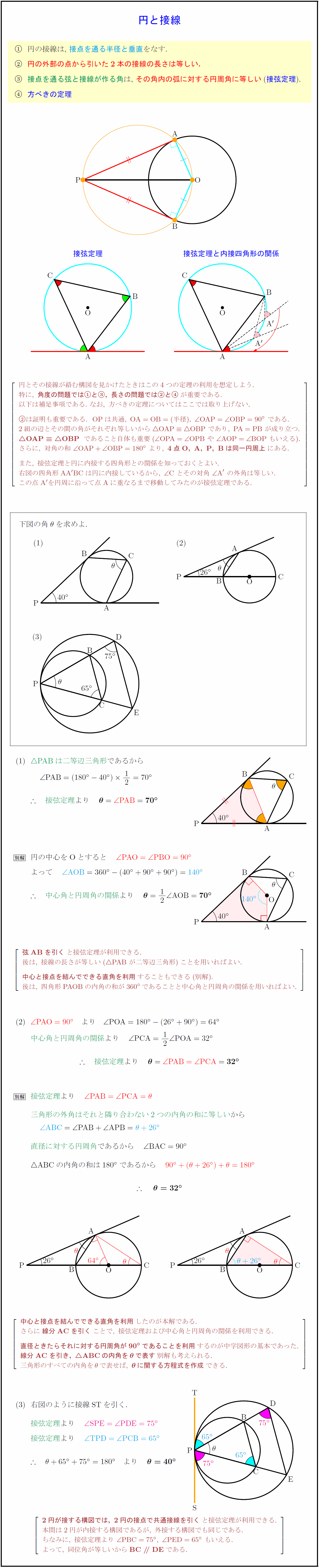
円の接線は,\ 接点を通る半径と垂直をなす. 円の外部の点から引いた2本の接線の長さは等しい. 接点を通る弦と接線が作る角は,\ その角内の弧に対する円周角に等しい(接弦定理). 方べきの定理接弦定理と内接四角形の関係 円とその接線が絡む構図を見かけたときはこの4つの定理の利用を想定しよう. 特に,\ {角度の問題ではと,\ 長さの問題ではと}が重要である. 以下は補足事項である.\ なお,\ 方べきの定理についてはここでは取り上げない. は証明も重要である.{OPは共通,\ OA=OB=(半径),\ ∠ OAP=∠ OBP=90°}\ である. 2組の辺とその間の角がそれぞれ等しいから{ OAP≡ OBP\ であり,\ PA=PB}\ が成り立つ. OAP≡ OBP\ }であること自体も重要(∠ OPA=∠ OPB\ や\ ∠ AOP=∠ BOP\ もいえる).} さらに,\ 対角の和\ {∠ OAP+∠ OBP=180°\ より,\ {4点O,\ A,\ P,\ Bは同一円周上}にある.} また,\ 接弦定理と円に内接する四角形との関係を知っておくとよい. 右図の四角形{AA}'{BC}は円に内接しているから,\ {∠ C\ とその対角\ ∠ A}’\ の外角は等しい. この点 A’を円周に沿って点 Aに重なるまで移動してみたのが接弦定理である. 二等辺三角形}であるから 中心角と円周角の関係 {弦{AB}を引く}と接弦定理が利用できる. 後は,\ 接線の長さが等しい({ PAB}\ が二等辺三角形)ことを用いればよい. {中心と接点を結んでできる直角を利用}することもできる(別解). 後は,\ 四角形{PAOB}の内角の和が360°であることと中心角と円周角の関係を用いればよい. {接弦定理}より三角形の外角はそれと隣り合わない2つの内角の和に等しい}から 直径に対する円周角}であるから \D[sw]{B} \E[e]{C} \O[s]{O} } $[l} {中心と接点を結んでできる直角を利用}したのが本解である. さらに{線分{AC}を引く}ことで,\ 接弦定理および中心角と円周角の関係を利用できる. {直径ときたらそれに対する円周角が90°であることを利用}するのが中学図形の基本であった. {線分{AC}を引き,\ { ABC}の内角をθで表す}別解も考えられる. 三角形のすべての内角をθで表せば,\ {θに関する方程式を作成}できる. }]$ 右図のように接線STを引く. {2円が接する構図では,\ 2円の接点で共通接線を引く}と接弦定理が利用できる. 本問は2円が内接する構図であるが,\ 外接する構図でも同じである. ちなみに,\ 接弦定理より\ {∠ PBC=75°,\ ∠ PED=65°}\ もいえる. よって,\ 同位角が等しいからBC∥ DEである.

