当ページは、2次曲線カテゴリと極座標・極方程式カテゴリの両方に属しています。通常は極方程式分野で学習する内容です。
(2)の問題の「原点」は「焦点」の誤りですm(_ _)m
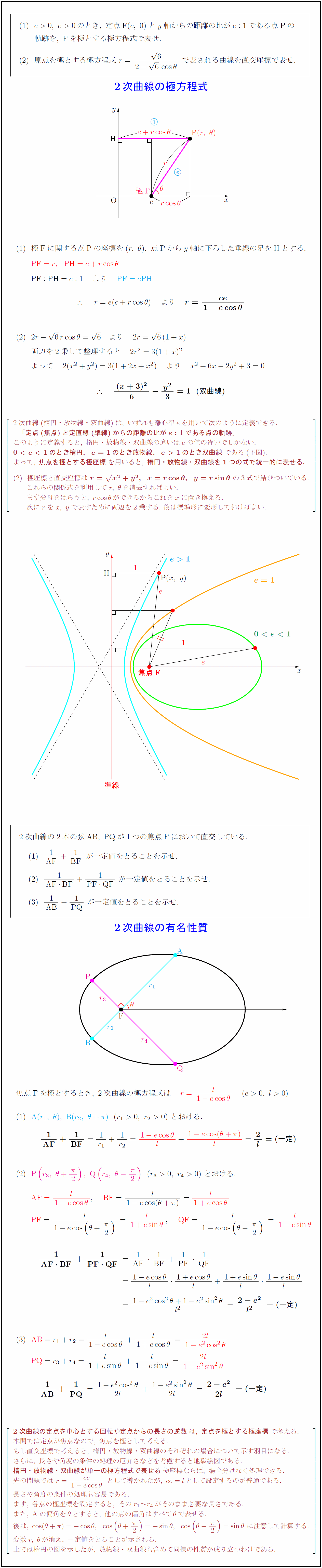
定点{F}(c,\ 0)とy軸からの距離の比がe:1である点{P}の$ $軌跡を,\ {F}を極とする極方程式で表せ.$ $原点を極とする極方程式\ r={6}{2-6cosθ}\ で表される曲線を直交座標で表せ.$ $極{F}に関する点{P}の座標を(r,\ θ),\ 点{P}からy軸に下ろした垂線の足を{H}とする.$ ${PF=r},{PH}=c+rcosθ}$ ${PF:PH}=e:1 より {PF=ePH$ $ r=e(c+rcosθ) より {r={ce}{1-ecosθ$} $2r-6rcosθ=6 より 2r=6(1+x)$ $両辺を2乗して整理すると 2r²=3(1+x)²$ $よって 2(x²+y²)=3(1+2x+x²) より x²+6x-2y²+3=0$ $ (x+3)²}{6}-{y²}{3}=1(双曲線)}$} $[l} 2次曲線(楕円・放物線・双曲線)は,\ いずれも離心率eを用いて次のように定義できる. {「定点(焦点)と定直線(準線)からの距離の比がe:1である点の軌跡}」 このように定義すると,\ 楕円・放物線・双曲線の違いはeの値の違いでしかない. {のとき楕円,e=1のとき放物線,のとき双曲線}である(下図). よって,\ {焦点を極とする極座標}を用いると,\ {楕円・放物線・双曲線を1つの式で統一的に表せる.} 極座標と直交座標は\ {r={x²+y²},x=rcosθ,y=rsinθ}\ の3式で結びついている. これらの関係式を利用してr,\ θを消去すればよい. まず分母をはらうと,\ rcosθができるからこれをxに置き換える. 次にrをx,\ yで表すために両辺を2乗する.\ 後は標準形に変形しておけばよい. 準線2次曲線の2本の弦{AB,\ PQ}が1つの焦点{F}において直交している.$ $1}{AF}+{1}{BF\ が一定値をとることを示せ.$ $1}{AF BF}+{1}{PF QF\ が一定値をとることを示せ.$ $1}{AB}+{1}{PQ\ が一定値をとることを示せ.$ 焦点{F}を極とするとき,\ 2次曲線の極方程式は {2次曲線の定点を中心とする回転や定点からの長さの逆数}は,\ {定点を極とする極座標}で考える. 本問では定点が焦点なので,\ 焦点を極として考える. もし直交座標で考えると,\ 楕円・放物線・双曲線のそれぞれの場合について示す羽目になる. さらに,\ 長さや角度の条件の処理の厄介さなどを考慮すると地獄絵図である. {楕円・放物線・双曲線が単一の極方程式で表せる}極座標ならば,\ 場合分けなく処理できる. 先の問題では\ r={ce}{1-ecosθ}\ として導かれたが,\ ce=lとして設定するのが普通である. 長さや角度の条件の処理も容易である. まず,\ 各点の極座標を設定すると,\ そのr₁~r₄がそのまま必要な長さである. また,\ {A}の偏角をθとすると,\ 他の点の偏角はすべてθで表せる. 後は,\ cos(θ+π)=-cosθ,cos(θ+{π}{2})=-sinθ,cos(θ-{π}{2})=sinθ\ に注意して計算する. 変数r,\ θが消え,\ 一定値をとることが示される. 上では楕円の図を示したが,\ 放物線・双曲線も含めて同様の性質が成り立つわけである.

