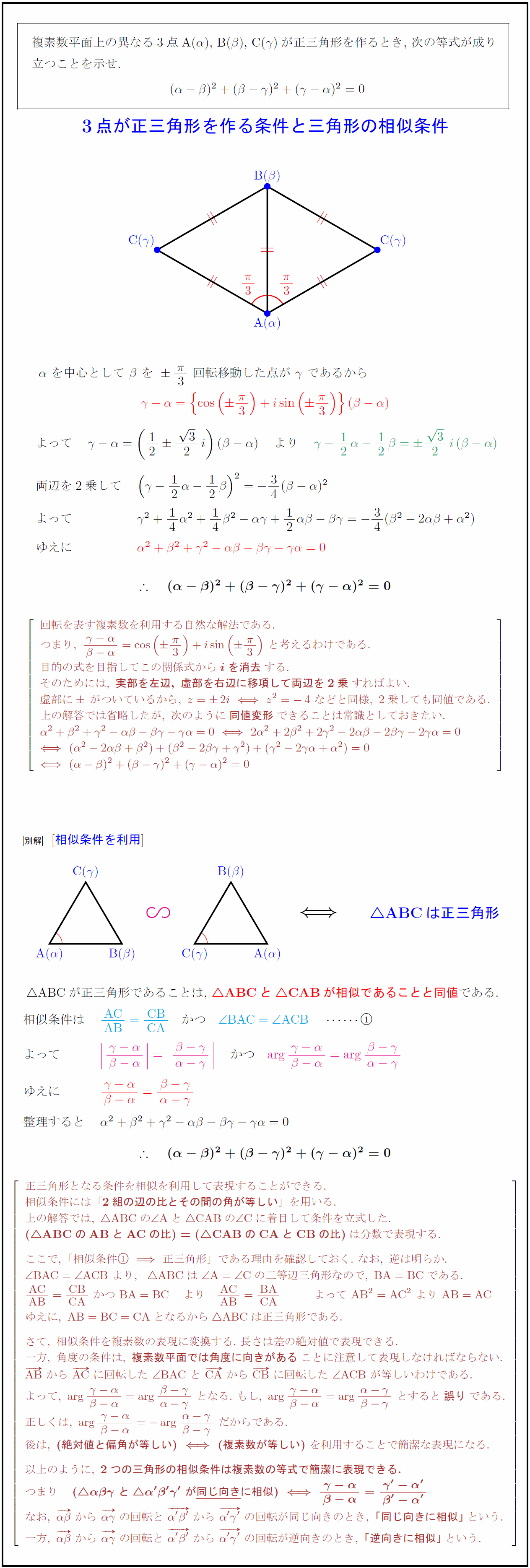
複素数平面上の異なる3点A($α$),\ B($β$),\ C($γ$)が正三角形を作るとき,\ 次の等式が成り }{A($α$) \end{pszahyou* $α\ を中心として\ β\ を\ {π}{3}\ 回転移動した点が\ γ\ であるから$ 回転を表す複素数を利用する自然な解法である. 目的の式を目指してこの関係式から{iを消去}する. そのためには,\ {実部を左辺,\ 虚部を右辺に移項して両辺を2乗}すればよい. 虚部にがついているから,\ z=2iz²=-4\ などと同様,\ 2乗しても同値である. 上の解答では省略したが,\ 次のように{同値変形}できることは常識としておきたい. $$ABCが正三角形であることは,\ Bが相似であることと同値である. $[l} 正三角形となる条件を相似を利用して表現することができる. 相似条件には「{2組の辺の比とその間の角が等しい}」を用いる. 上の解答では,\ \に着目して条件を立式した. は分数で表現する. ここで,\ 「相似条件正三角形」である理由を確認しておく.\ なお,\ 逆は明らか. さて,\ 相似条件を複素数の表現に変換する.\ 長さは差の絶対値で表現できる. 一方,\ 角度の条件は,\ {複素数平面では角度に向きがある}ことに注意して表現しなければならない. AB}\ から\ AC}\ に回転した\ ∠{BAC}\ と\ CA}\ から\ CB}\ に回転した\ ∠{ACB}\ が等しいわけである. %三角形の形状決定では,\ 複素数\ {γ-α}{β-α}\ から\ 絶対値と偏角の情報を取り出した. 後は,\ {(絶対値と偏角が等しい)(複素数が等しい)}\ を利用することで簡潔な表現になる. 以上のように,\ {2つの三角形の相似条件は複素数の等式で簡潔に表現できる.} の回転が同じ向きのとき,\ {「同じ向きに相似」}という. 一方,\ の回転が逆向きのとき,\ {「逆向きに相似」}という.

