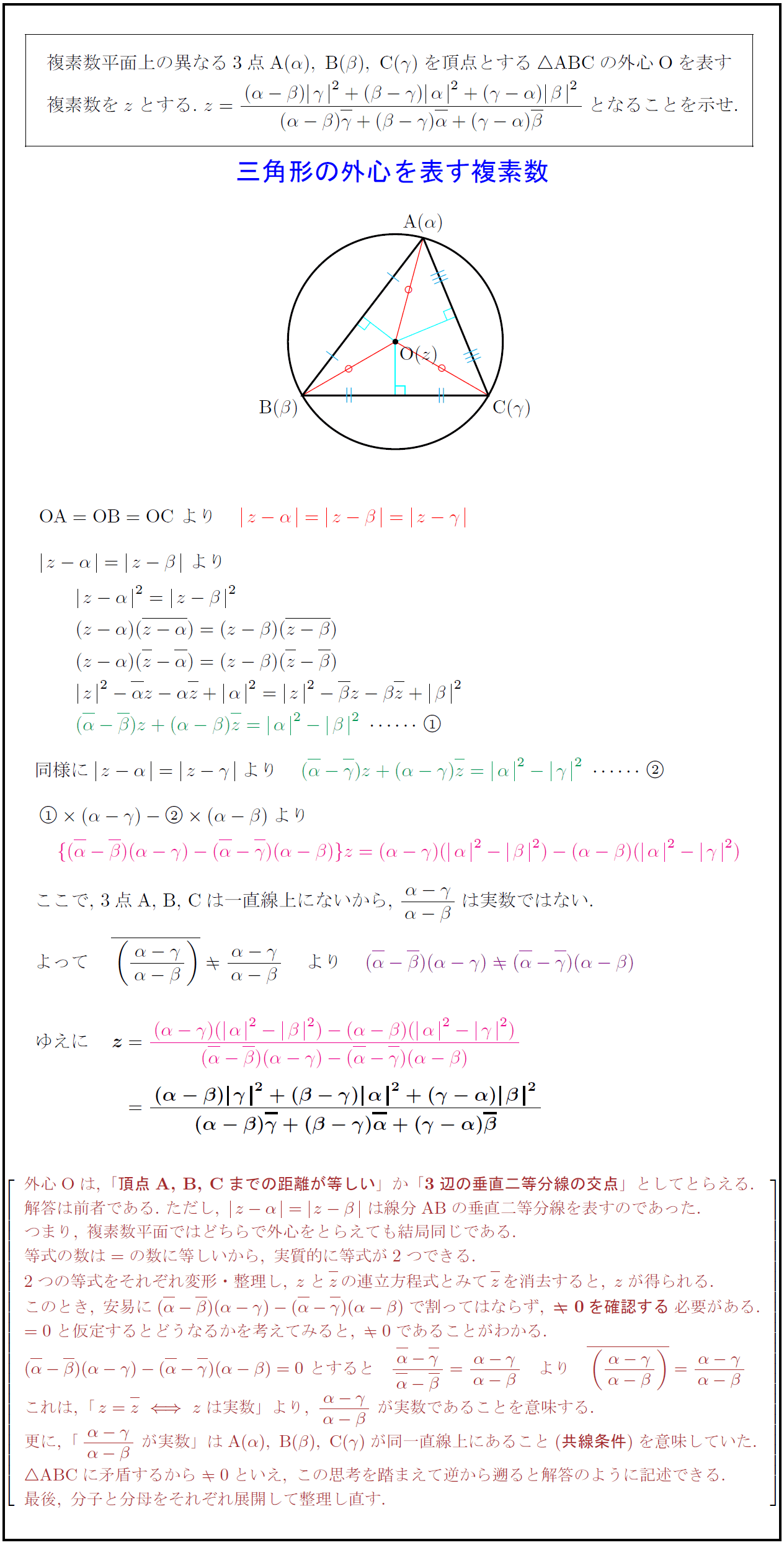
複素数平面上の異なる3点${A(α),\ B(β),\ C(γ)}$を頂点とする$$ABCの外心Oを表す 複素数を$z$とする.\ $z={(α-β)γ}²+(β-γ)α}²+(γ-α)β}²}{(α-β)γ+(β-γ)α+(γ-α)β}$となることを示せ. 三角形の外心を表す複素数} ここで,\ 3点A,\ B,\ Cは一直線上にないから,\ ${α-γ}{α-β}$は実数ではない. 外心 Oは,\ 「{頂点A,\ B,\ C}までの距離が等しい}」か「{3辺の垂直二等分線の交点}」としてとらえる. 解答は前者である.\ ただし,\ z-α}=z-β}\ は線分AB}の垂直二等分線を表すのであった. つまり,\ 複素数平面ではどちらで外心をとらえても結局同じである. 等式の数は=の数に等しいから,\ 実質的に等式が2つできる. 2つの等式をそれぞれ変形・整理し,\ zと zの連立方程式とみて zを消去すると,\ zが得られる. このとき,\ 安易に(α-β)(α-γ)-(α-γ)(α-β)で割ってはならず,\ {0を確認する}必要がある. =0と仮定するとどうなるかを考えてみると,\ 0であることがわかる これは,\ 「z= zzは実数」より,\ {α-γ}{α-β}\ が実数であることを意味する. 更に,\ 「{α-γ}{α-β}\ が実数」は{A(α),\ B(β),\ C(γ)}が同一直線上にあること({共線条件})を意味していた. ABC}に矛盾するから0といえ,\ この思考を踏まえて逆から遡ると解答のように記述できる. 最後,\ 分子と分母をそれぞれ展開して整理し直す.

