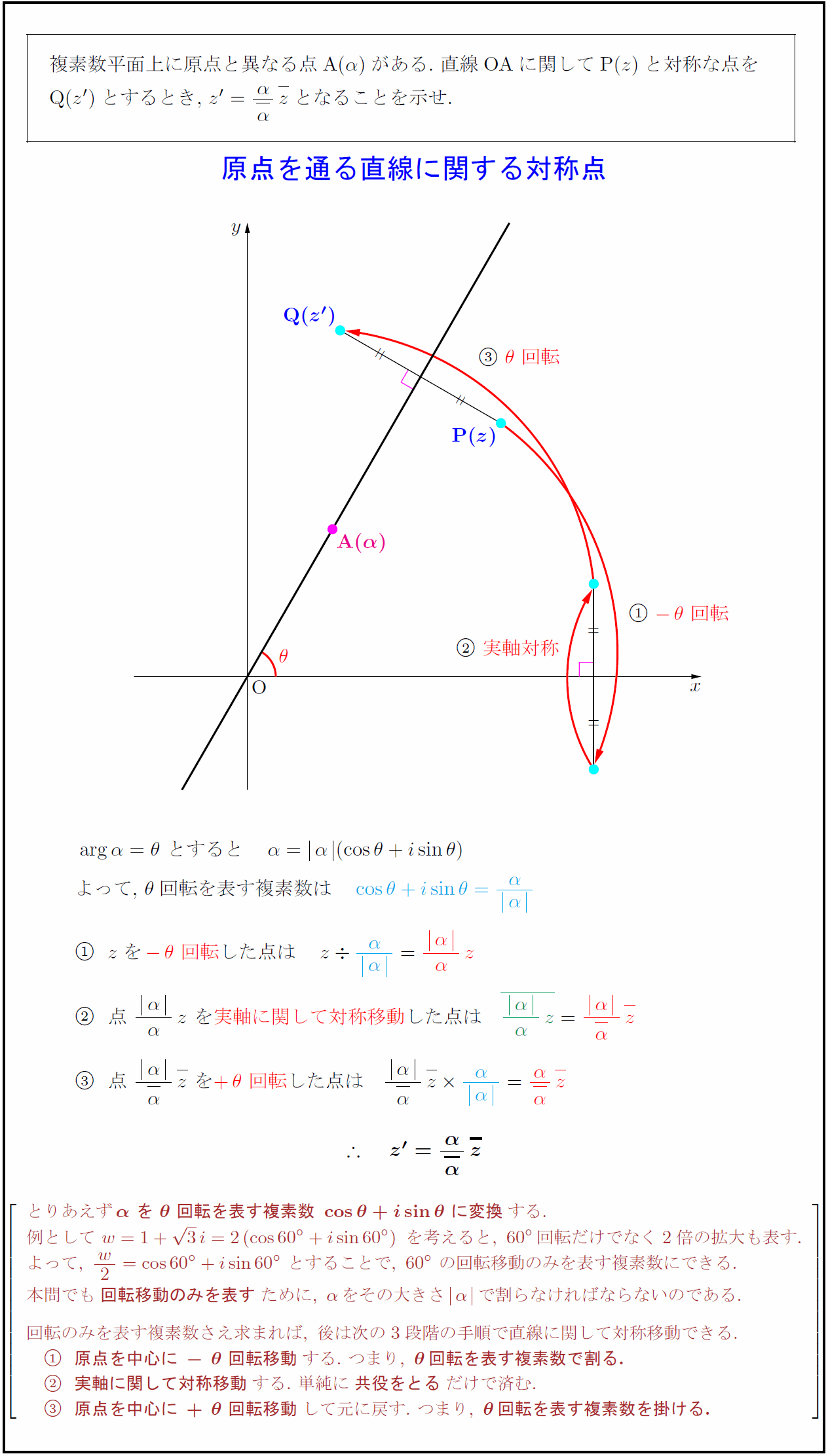
複素数平面上に原点と異なる点A($α$)がある.\ 直線OAに関してP($z$)と対称な点を }{実軸に関して対称移動}した点は とりあえず{α\ を\ θ\ 回転を表す複素数\ {θ}\ に変換}する. 例として\ w={1}+{√3}={60°}\ を考えると,\ 60°回転だけでなく2倍の拡大も表す. よって,\ {w}{2}={60°}\ とすることで,\ 60°\ の回転移動のみを表す複素数にできる. 本問でも{回転移動のみを表す}ために,\ αをその大きさα}で割らなければならないのである. 回転のみを表す複素数さえ求まれば,\ 後は次の3段階の手順で直線に関して対称移動できる. {原点を中心に-θ\ 回転移動}する.\ つまり,\ {θ 回転を表す複素数で割る.} {実軸に関して対称移動}する.\ 単純に{共役をとる}だけで済む. {原点を中心に+θ\ 回転移動}して元に戻す.\ つまり,\ {θ 回転を表す複素数を掛ける.}

