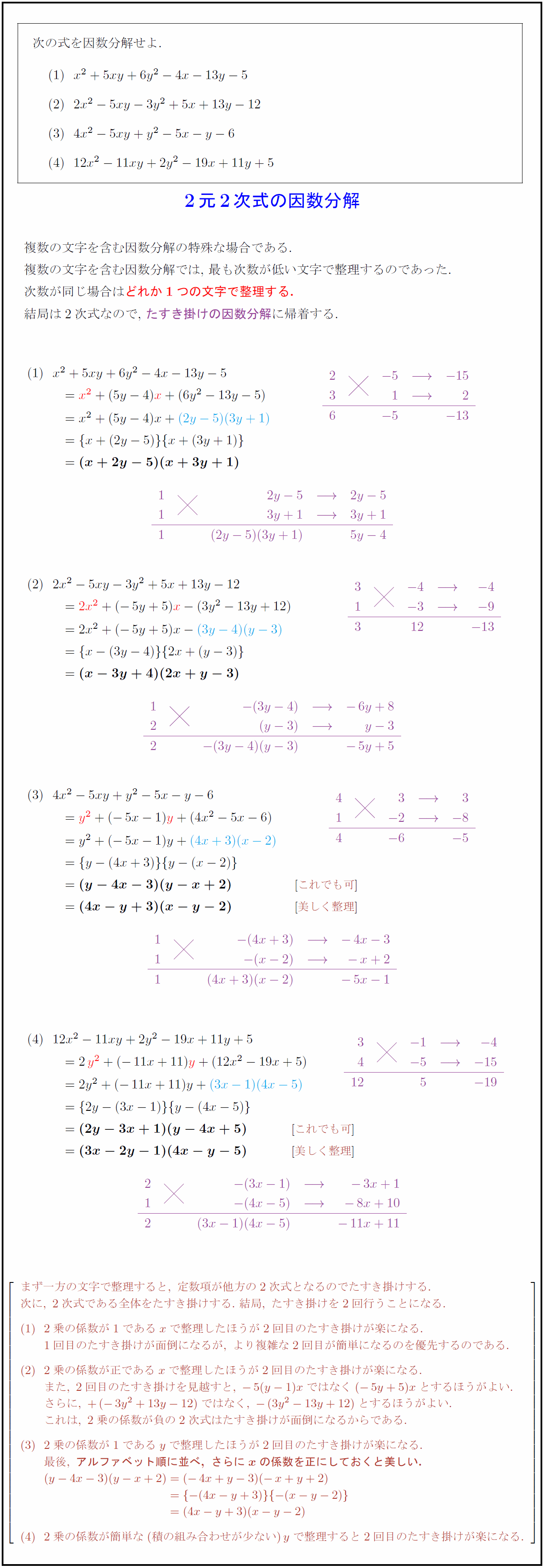
複数の文字を含む因数分解の特殊な場合である.
複数の文字を含む因数分解では,\ 最も次数が低い文字で整理するのであった.
次数が同じ場合は\どれか1つの文字で整理する.
結局は2次式なので,\たすき掛けの因数分解に帰着する.
まず一方の文字で整理すると,\ 定数項が他方の2次式となるのでたすき掛けする.
次に,\ 2次式である全体をたすき掛けする.\ 結局,\ たすき掛けを2回行うことになる.
(1)\ \ 2乗の係数が1であるxで整理したほうが2回目のたすき掛けが楽になる.
\ \ 1回目のたすき掛けが面倒になるが,\ より複雑な2回目が簡単になるのを優先するのである.
(2)\ \ 2乗の係数が正であるxで整理したほうが2回目のたすき掛けが楽になる.
\ \ また,\ 2回目のたすき掛けを見越すと,\ -\,5(y-1)xではなく(-\,5y+5)xとするほうがよい.
\ \ さらに,\ +\,(-\,3y^2+13y-12)ではなく,\ -\,(3y^2-13y+12)とするほうがよい.
\ \ これは,\ 2乗の係数が負の2次式はたすき掛けが面倒になるからである.
(3)\ \ 2乗の係数が1であるyで整理したほうが2回目のたすき掛けが楽になる.
\ \ 最後,\ アルファベット順に並べ,\ さらにxの係数を正にしておくと美しい.}
(4)\ \ 2乗の係数が簡単な(積の組み合わせが少ない)\,yで整理すると2回目のたすき掛けが楽になる.

