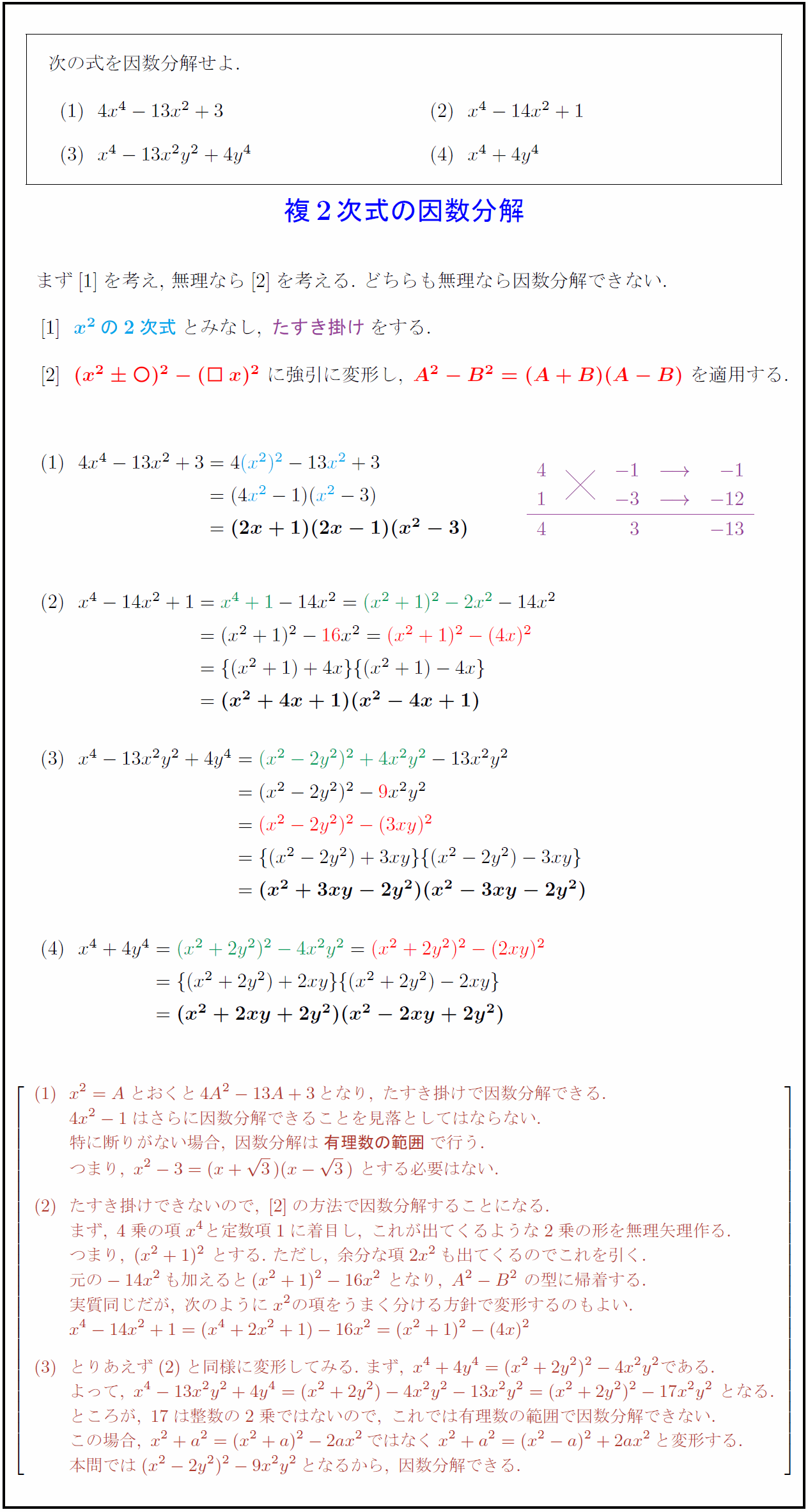
(3)の解説で (x²+2y²) とありますが、(x²+2y²)² の誤りですm(_ _)m
まず$$を考え,\ 無理なら$$を考える.\ どちらも無理なら因数分解できない.
$$${x²の2次式とみなし,\ {たすき掛けをする.$
$$${(x²○)²-(□x)²\ に強引に変形し,\ {A²-B²=(A+B)(A-B)\ を適用する.$
x²=Aとおくと4A²-13A+3となり,\ たすき掛けで因数分解できる.
4x²-1はさらに因数分解できることを見落としてはならない.
特に断りがない場合,\ 因数分解は{有理数の範囲}で行う.
つまり,\ x²-3=(x+3)(x-3)\ とする必要はない.
たすき掛けできないので,\ の方法で因数分解することになる.
まず,\ 4乗の項x⁴と定数項1に着目し,\ これが出てくるような2乗の形を無理矢理作る.
つまり,\ (x²+1)²\ とする.\ ただし,\ 余分な項2x²も出てくるのでこれを引く.
元の-14x²も加えると(x²+1)²-16x²\ となり,\ A²-B²\ の型に帰着する.
実質同じだが,\ 次のようにx²の項をうまく分ける方針で変形するのもよい.
x⁴-14x²+1=(x⁴+2x²+1)-16x²=(x²+1)²-(4x)²
とりあえずと同様に変形してみる.\ まず,\ x⁴+4y⁴=(x²+2y²)²-4x²y²である.
よって,\ x⁴-13x²y²+4y⁴=(x²+2y²)-4x²y²-13x²y²=(x²+2y²)²-17x²y²\ となる.
ところが,\ 17は整数の2乗ではないので,\ これでは有理数の範囲で因数分解できない.
この場合,\ x²+a²=(x²+a)²-2ax²ではなくx²+a²=(x²-a)²+2ax²と変形する.
本問では(x²-2y²)²-9x²y²となるから,\ 因数分解できる.
$$${x²の2次式とみなし,\ {たすき掛けをする.$
$$${(x²○)²-(□x)²\ に強引に変形し,\ {A²-B²=(A+B)(A-B)\ を適用する.$
x²=Aとおくと4A²-13A+3となり,\ たすき掛けで因数分解できる.
4x²-1はさらに因数分解できることを見落としてはならない.
特に断りがない場合,\ 因数分解は{有理数の範囲}で行う.
つまり,\ x²-3=(x+3)(x-3)\ とする必要はない.
たすき掛けできないので,\ の方法で因数分解することになる.
まず,\ 4乗の項x⁴と定数項1に着目し,\ これが出てくるような2乗の形を無理矢理作る.
つまり,\ (x²+1)²\ とする.\ ただし,\ 余分な項2x²も出てくるのでこれを引く.
元の-14x²も加えると(x²+1)²-16x²\ となり,\ A²-B²\ の型に帰着する.
実質同じだが,\ 次のようにx²の項をうまく分ける方針で変形するのもよい.
x⁴-14x²+1=(x⁴+2x²+1)-16x²=(x²+1)²-(4x)²
とりあえずと同様に変形してみる.\ まず,\ x⁴+4y⁴=(x²+2y²)²-4x²y²である.
よって,\ x⁴-13x²y²+4y⁴=(x²+2y²)-4x²y²-13x²y²=(x²+2y²)²-17x²y²\ となる.
ところが,\ 17は整数の2乗ではないので,\ これでは有理数の範囲で因数分解できない.
この場合,\ x²+a²=(x²+a)²-2ax²ではなくx²+a²=(x²-a)²+2ax²と変形する.
本問では(x²-2y²)²-9x²y²となるから,\ 因数分解できる.

