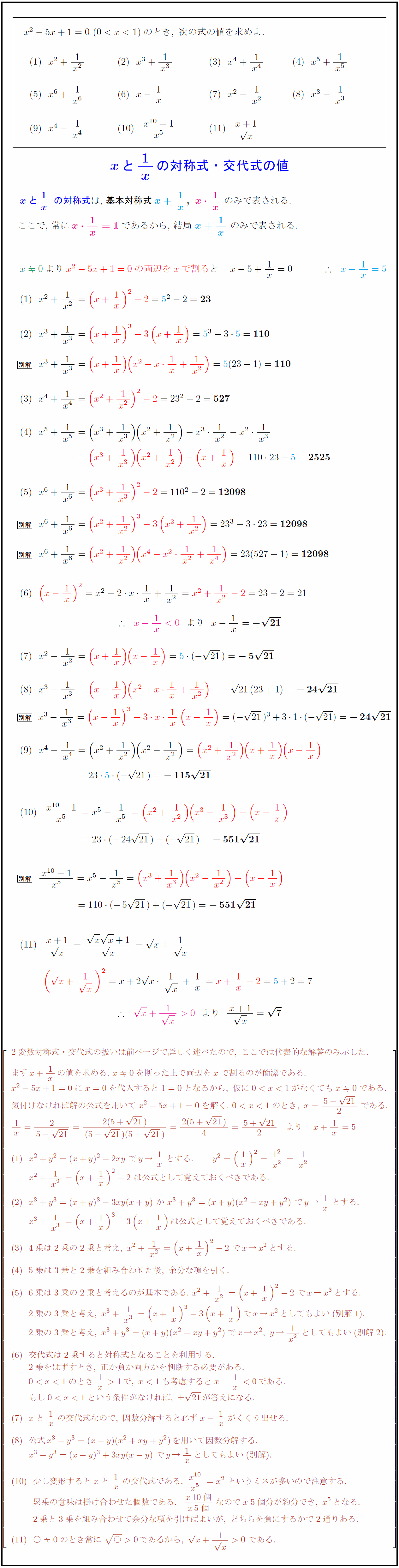
x²-5x+1=0\のとき,\ 次の式の値を求めよ.$ $の対称式・交代式の値 の対称式は,\ 基本対称式$}$}のみで表される. x²-5x+1=0の両辺をxで割る} 2変数対称式・交代式の扱いは前ページで詳しく述べたので,\ ここでは代表的な解答のみ示した. まずx+1xの値を求める.\ x0を断った上で}両辺をxで割るのが簡潔である. x²-5x+1=0にx=0を代入すると1=0となるから,\ 仮になくてもx0である. 気付けなければ解の公式を用いてx²-5x+1=0を解く.\のとき,\ x={5-{21{2}\ である. は公式として覚えておくべきである. x³+y³=(x+y)³-3xy(x+y)\ か\ x³+y³=(x+y)(x²-xy+y²)\ 4乗は2乗の2乗と考え,\ x²+{1}{x²}=(x+1x)²-2\ でx→x²とする. 5乗は3乗と2乗を組み合わせた後,\ 余分な項を引く. 6乗は3乗の2乗と考えるのが基本である.\ x²+{1}{x²}=(x+1x)²-2\ でx→x³とする. 2乗の3乗と考え,\ x³+{1}{x³}=(x+1x)³-3(x+1x)でx→x²としてもよい(別解1). 2乗の3乗と考え,\ x³+y³=(x+y)(x²-xy+y²)でx→x²,\ y→{1}{x²}としてもよい(別解2). 交代式は2乗すると対称式となることを利用する. 2乗をはずすとき,\ 正か負か両方かを判断する必要がある. 考慮するとx-1x<0である. 条件がなければ,\ {21}が答えになる. xと1xの交代式なので,\ 因数分解すると必ずx-1xがくくり出せる. 公式x³-y³=(x-y)(x²+xy+y²)を用いて因数分解する. x³-y³=(x-y)³+3xy(x-y)\ でy→1xとしてもよい(別解). 少し変形するとxと1xの交代式である.\ {x^{10{x⁵}=x²\ というミスが多いので注意する. {(11)}累乗の意味は掛け合わせた個数である.{x10個}{x5個}なのでx\;5個分が約分でき,\ x⁵となる. {(11)}2乗と3乗を組み合わせて余分な項を引けばよいが,\ どちらを負にするかで2通りある. (11)○0のとき常に\ {○}>0であるから,\ x+{1}{ x}>0\ である.

