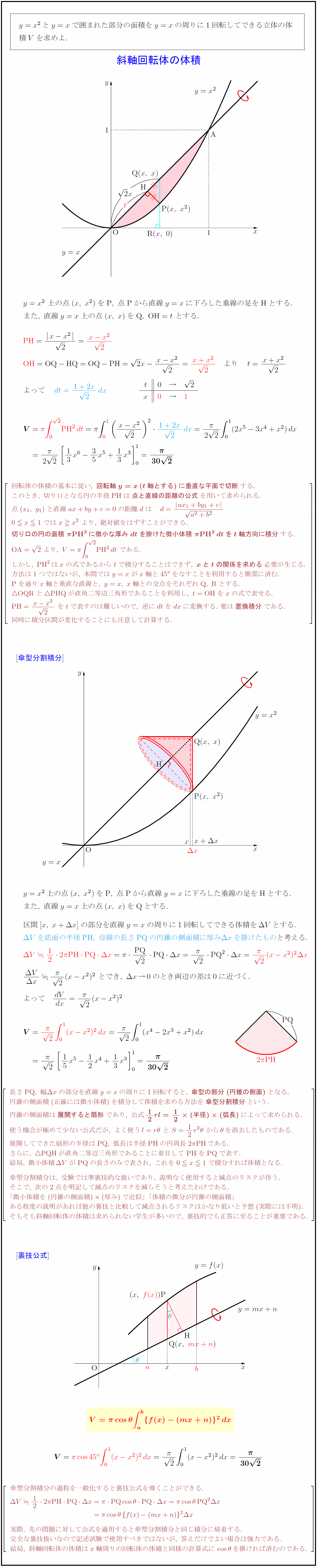
y=x²とy=xで囲まれた部分の面積をy=xの周りに1回転してできる立体の体$ $積Vを求めよ.$ $y=x²\ 上の点(x,\ x²)を{P},\ 点{P}から直線y=xに下ろした垂線の足を{H}とする.$ 回転体の体積の基本に従い,\ {回転軸y=x(t軸とする)に垂直な平面で切断}する. このとき,\ 切り口となる円の半径{PH}は{点と直線の距離の公式}を用いて求められる. 点(x₁,\ y₁)と直線ax+by+c=0の距離dは d={ax₁+by₁+ca²+b² 0 x1\ ではx x²\ より,\ 絶対値をはずすことができる. {切り口の円の面積\ π{PH}²に微小な厚みdtを掛けた微小体積\ π{PH}²dtをt軸方向に積分}する. {OA}=2\ より,\ V=π∫PH}²dt\ である. しかし,\ {PH}²はxの式であるからtで積分することはできず,\ {xとtの関係を求める}必要が生じる. 方法は1つではないが,\ 本問ではy=xがx軸と45°をなすことを利用すると簡潔に済む. {P}を通りx軸と垂直な直線と,\ y=x,\ x軸との交点をそれぞれ{Q,\ R}とする. {OQR}と{PHQ}が直角二等辺三角形であることを利用し,\ t={OH}をxの式で表せる. {PH}={x-x²}{2}\ をtで表すのは難しいので,\ 逆にdtをdxに変換する.\ 要は{置換積分}である. 同時に積分区間が変化することにも注意して計算する. $y=x²上の点(x,\ x²)を{P},\ 点{P}から直線y=xに下ろした垂線の足を{H}とする.$ $また,\ 直線y=x上の点(x,\ x)を{Q}とする.$ $区間[x,\ x+Δ x]の部分を直線y=xの周りに1回転してできる体積をΔ Vとする.$ .98}{$Δ Vを底面の半径{PH},\ 母線の長さ{PQ}の円錐の側面積に厚みΔ xを掛けたもの}と考える.$} 長さ{PQ},\ 幅Δ xの部分を直線y=xの周りに1回転すると,\ {傘型の部分(円錐の側面)}となる. 円錐の側面積(正確には微小体積)を積分して体積を求める方法を{傘型分割積分}という. 円錐の側面積は{展開すると扇形}であり,\ 公式{12rl=12(半径)(弧長)}によって求められる. 使う機会が極めて少ない公式だが,\ よく使うl=rθ\ と\ S=12r²θ\ からθを消去したものである. 展開してできた扇形の半径は{PQ},\ 弧長は半径{PH}の円周長2π{PH}である. さらに,\ {PQH}が直角二等辺三角形であることに着目して\ {PH}を{PQ}で表す. 結局,\ 微小体積Δ Vが{PQ}の長さのみで表され,\ これを0 x1で積分すれば体積となる. 傘型分割積分は,\ 受験では準裏技的な扱いであり,\ 説明なく使用すると減点のリスクが伴う. そこで,\ 次の2点を明記して減点のリスクを減らそうと考えたわけである. 「微小体積を(円錐の側面積)(厚み)で近似」「体積の微分が円錐の側面積」 ある程度の説明があれば他の裏技と比較して減点されるリスクはかなり低いと予想(実際には不明). そもそも斜軸回転体の体積は求められない学生が多いので,\ 裏技的でも正答に至ることが重要である. 傘型分割積分の過程を一般化すると裏技公式を導くことができる. 実際,\ 先の問題に対して公式を適用すると傘型分割積分と同じ積分に帰着する. 完全な裏技扱いなので記述試験で使用すべきではないが,\ 答えだけでよい場合は強力である. 結局,\ 斜軸回転体の体積はx軸周りの回転体の体積と同様の計算式にcosθを掛ければ済むのである.

