(4)の問題文が「点(2,1)を通る円」となっていますが、「点(-2,1)を通る円」の誤りですm(_ _)m
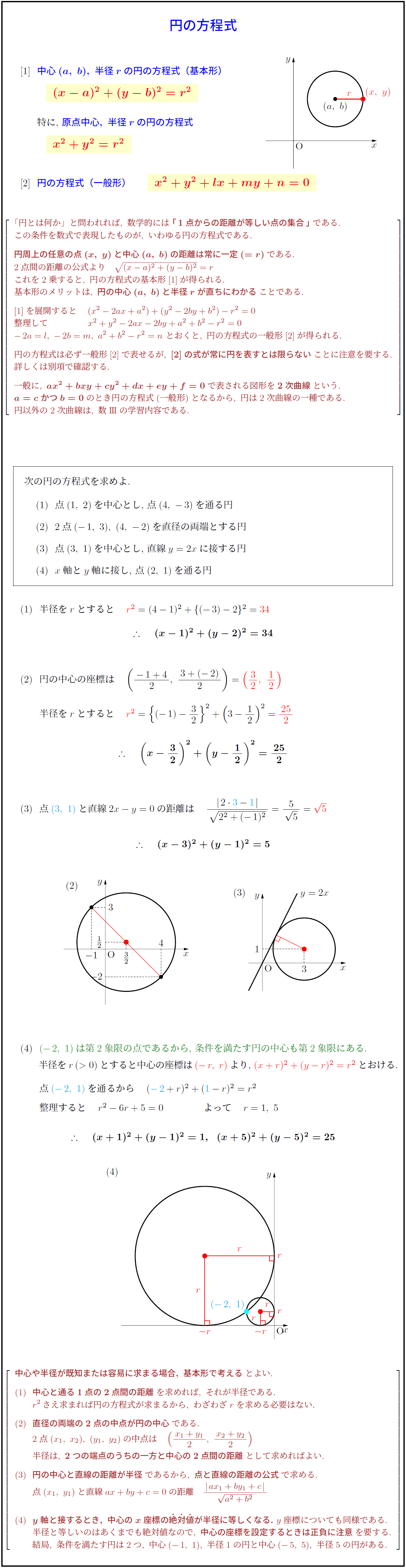
中心(a,\ b),\ 半径rの円の方程式(基本形)}{原点中心,\ 半径rの円の方程式}{x^2+y^2+lx+my+n=0
「円とは何か」と問われれば,\ 数学的には「\,1点からの距離が等しい点の集合\,」}である.
この条件を数式で表現したものが,\ いわゆる円の方程式である.
円周上の任意の点(x,\ y)と中心(a,\ b)の距離は常に一定(=r)}である.
2点間の距離の公式より √{(x-a)^2+(y-b)^2}=r
これを2乗すると,\ 円の方程式の基本形[1]が得られる.
基本形のメリットは,\ 円の中心(a,\ b)と半径rが直ちにわかる}ことである.
[1]}を展開すると (x^2-2ax+a^2)+(y^2-2by+b^2)-r^2=0
整理して \ \ x^2+y^2-2ax-2by+a^2+b^2-r^2=0
-\,2a=l,\ -\,2b=m,\ a^2+b^2-r^2=n\ とおくと,\ 円の方程式の一般形[2]が得られる.
円の方程式は必ず一般形[2]で表せるが,\ [2]の式が常に円を表すとは限らない}ことに注意を要する.
詳しくは別項で確認する.
一般に,\ ax^2+bxy+cy^2+dx+ey+f=0}で表される図形を2次曲線}という.
a=cかつb=0}のとき円の方程式(一般形)となるから,\ 円は2次曲線の一種である.
円以外の2次曲線は,\ 数III}の学習内容である.
次の円の方程式を求めよ.
(1)\ \ 点$(1,\ 2)$を中心とし,\ 点$(4,\ -\,3)$を通る円
(2)\ \ 2点$(-\,1,\ 3),\ (4,\ -\,2)$を直径の両端とする円
(3)\ \ 点$(3,\ 1)$を中心とし,\ 直線$y=2x$に接する円
(4)\ \ $x$軸と$y$軸に接し,\ 点$(-\,2,\ 1)$を通る円 \\
(2)\ \ 円の中心の座標は
(3)\ \ 点$(3,\ 1)}$と直線$2x-y=0$の距離は $は第2象限の点であるから,\ 条件を満たす円の中心も第2象限にある.}
半径を$r\,(とすると中心の座標は$(-\,r,\ r)$}より,\ $(x+r)^2+(y-r)^2=r^2}$とおける.
点$(-\,2,\ 1)}$を通るから $(-\,2}+r)^2+(1}-r)^2=r^2$
整理すると $r^2-6r+5=0$ よって $r=1,\ 5$
∴ (x+1)^2+(y-1)^2=1,\ \ (x+5)^2+(y-5)^2=25}$
中心や半径が既知または容易に求まる場合,\ 基本形で考える}とよい.
(1)\ \ 中心と通る1点の2点間の距離}を求めれば,\ それが半径である.
\ \ r^2\,さえ求まれば円の方程式が求まるから,\ わざわざrを求める必要はない.
(2)\ \ 直径の両端の2点の中点が円の中心}である.
\ \ 2点(x_1,\ x_2),\ (y_1,\ y_2)の中点は x_1+y_1}{2},\ x_2+y_2}{2}
\ \ 半径は,\ 2つの端点のうちの一方と中心の2点間の距離}として求めればよい.
(3)\ \ 円の中心と直線の距離が半径}であるから,\ 点と直線の距離の公式}で求める.
\ \ 点(x_1,\ y_1)と直線ax+by+c=0の距離 ax_1+by_1+c{√{a^2+b^2
(4)\ \ y軸と接するとき,\ 中心のx座標の\dot{絶}\dot{対}\dot{値}が半径に等しくなる.}\ y座標についても同様である.
\ \ 半径と等しいのはあくまでも絶対値なので,\ 中心の座標を設定するときは正負に注意}を要する.
\ \ 結局,\ 条件を満たす円は2つ,\ 中心(-\,1,\ 1),\ 半径1の円と中心(-\,5,\ 5),\ 半径5の円がある.

