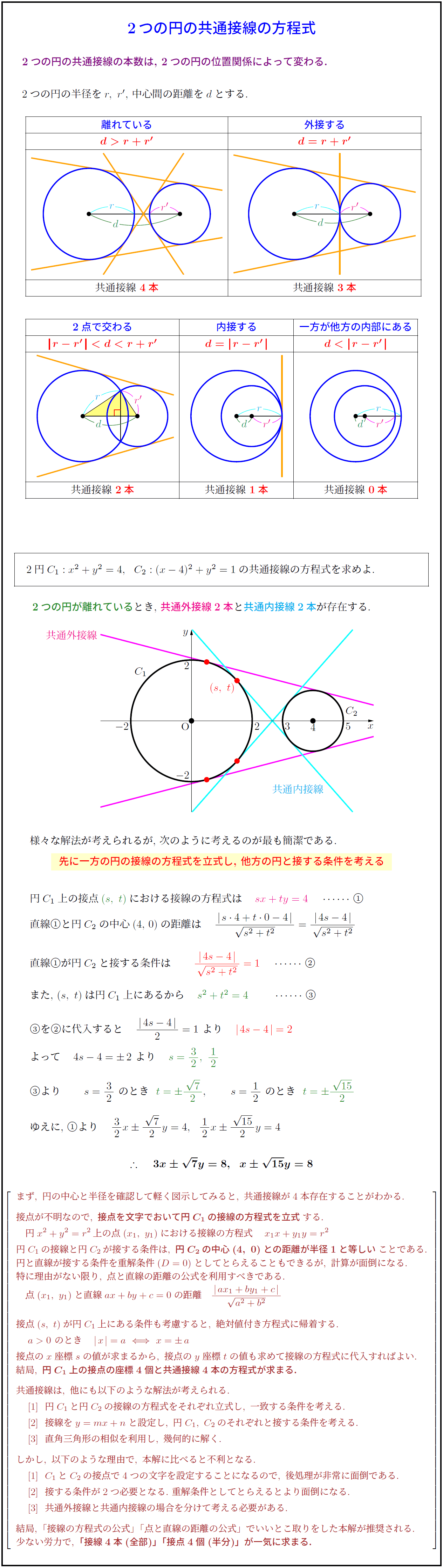
2つの円の共通接線の本数は,\ 2つの円の位置関係によって変わる.
2つの円の半径を$r,\ r’$,\ 中心間の距離を$d$とする.
離れている}{外接する}
共通接線\ 2本 & 共通接線\ 1本 & 共通接線\ 2円$C_1:x^2+y^2=4,\ \ C_2:(x-4)^2+y^2=1$の共通接線の方程式を求めよ.
2つの円が離れているとき,\ {共通外接線2本と\共通内接線2本が存在する.
様々な解法が考えられるが,\ 次のように考えるのが最も簡潔である.
\dilutecolor{yellow}{.2}{dyellow}\colorbox{dyellow}{\ 先に一方の円の接線の方程式を立式し,\ 他方の円と接する条件を考える\
まず,\ 円の中心と半径を確認して軽く図示してみると,\ 共通接線が4本存在することがわかる.
接点が不明なので,\ 接点を文字でおいて円C_1\,の接線の方程式を立式}する.
円x^2+y^2=r^2\,上の点(x_1,\ y_1)における接線の方程式 x_1x+y_1y=r^2
円C_1\,の接線と円C_2\,が接する条件は,\ 円C_2\,の中心(4,\ 0)との距離が半径1と等しい}ことである.
円と直線が接する条件を重解条件(D=0)としてとらえることもできるが,\ 計算が面倒になる.
特に理由がない限り,\ 点と直線の距離の公式を利用すべきである.
点(x_1,\ y_1)と直線ax+by+c=0の距離 ax_1+by_1+c{√{a^2+b^2
接点(s,\ t)が円C_1\,上にある条件も考慮すると,\ 絶対値付き方程式に帰着する.
a>0\ のとき x}=a\ ⇔\ x=±\,a
接点のx座標sの値が求まるから,\ 接点のy座標tの値も求めて接線の方程式に代入すればよい.
結局,\ 円C_1\,上の接点の座標4個と共通接線4本の方程式が求まる.}
共通接線は,\ 他にも以下のような解法が考えられる.
[1]\ \ 円C_1\,と円C_2\,の接線の方程式をそれぞれ立式し,\ 一致する条件を考える.
[2]\ \ 接線をy=mx+nと設定し,\ 円C_1,\ C_2\,のそれぞれと接する条件を考える.
[3]\ \ 直角三角形の相似を利用し,\ 幾何的に解く.
しかし,\ 以下のような理由で,\ 本解に比べると不利となる.
[1]\ \ C_1\,とC_2\,の接点で4つの文字を設定することになるので,\ 後処理が非常に面倒である.
[2]\ \ 接する条件が2つ必要となる.\ これを重解条件でとらえるとさらに面倒になる.
[3]\ \ 共通外接線と共通内接線の場合を分けて考える必要がある.
結局,\ 「接線の方程式の公式」「点と直線の距離の公式」でいいとこ取りをした本解が推奨される.
少ない労力で,\ 「接線4本(全部)」「接点4個(半分)」が一気に求まる.}

