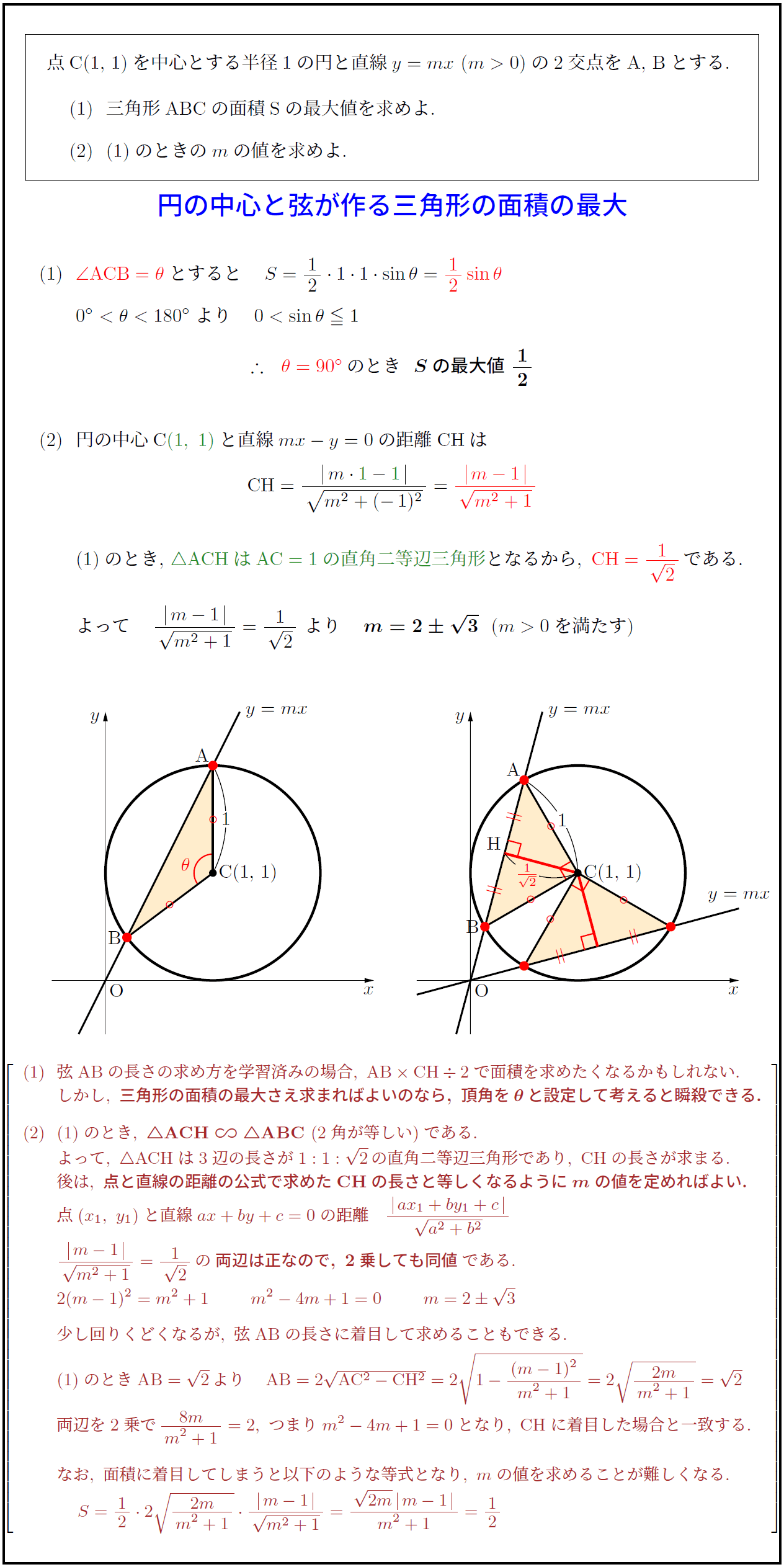
点C(1,\ 1)を中心とする半径1の円と直線$y=mx\ (m>0)$の2交点をA,\ Bとする.
(1)\ \ 三角形ABCの面積Sの最大値を求めよ.
(2)\ \ (1)のときの$m$の値を求めよ.円の中心と弦が作る三角形の面積の最大}triangle ACHはAC=1の直角二等辺三角形}となるから,\ CH=1}{√2\,である.}$
(1)\ \ 弦AB}の長さの求め方を学習済みの場合,\ AB}×CH}÷2で面積を求めたくなるかもしれない.
\ \ しかし,\ 三角形の面積の最大さえ求まればよいのなら,\ 頂角を\,θ\,と設定して考えると瞬殺できる.}
(2)\ \ (1)のとき,\ △ ACH∽ △ ABC\ (2角が等しい)である.
\ \ よって,\ △ACH}は3辺の長さが1:1:√2\,の直角二等辺三角形であり,\ CH}の長さが求まる.
\ \ 後は,\ 点と直線の距離の公式で求めたCH}の長さと等しくなるようにmの値を定めればよい.}
\ \ 点(x_1,\ y_1)と直線ax+by+c=0の距離 ax_1+by_1+cの両辺は正なので,\ 2乗しても同値}である.
\ \ 2(m-1)^2=m^2+1 m^2-4m+1=0 m=2±√3
\ \ 少し回りくどくなるが,\ 弦AB}の長さに着目して求めることもできる. \\
\ \ 両辺を2乗で\,8m}{m^2+1}=2,\ つまりm^2-4m+1=0となり,\ CH}に着目した場合と一致する.
\ \ なお,\ 面積に着目してしまうと以下のような等式となり,\ mの値を求めることが難しくなる. \

