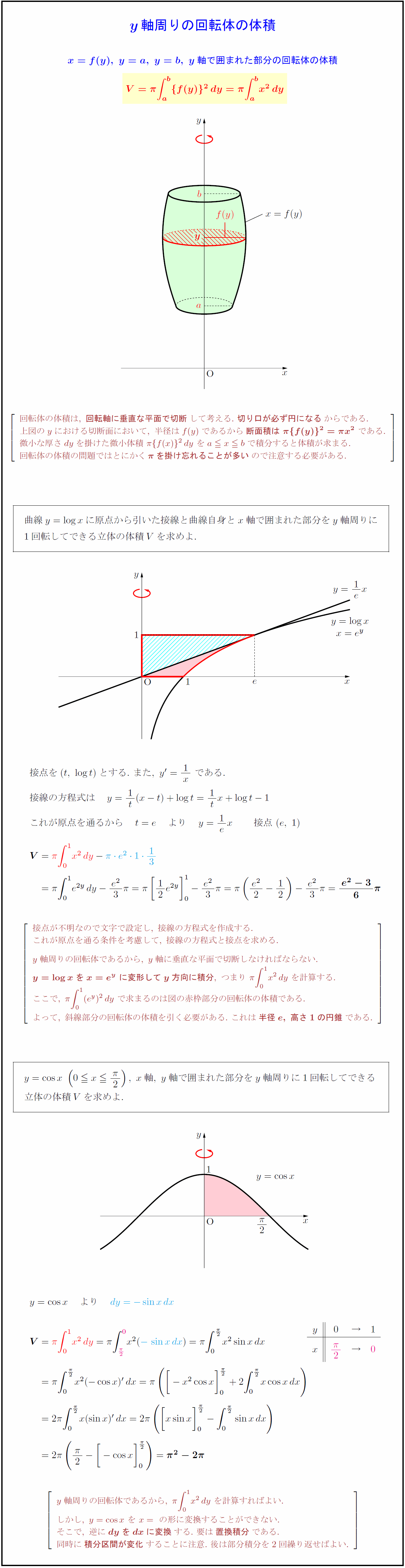
x=f(y),\ y=a,\ y=b,\ y軸で囲まれた部分の回転体の体積$} 回転体の体積は,\ {回転軸に垂直な平面で切断}して考える.\ {切り口が必ず円になる}からである. 上図のyにおける切断面において,\ 半径はf(y)であるから{断面積は\ π{f(y)}²=π x²}\ である. 微小な厚さdyを掛けた微小体積\ π{f(x)}²dy\ をa x bで積分すると体積が求まる. 回転体の体積の問題ではとにかく{πを掛け忘れることが多い}ので注意する必要がある. 曲線y=log xに原点から引いた接線と曲線自身とx軸で囲まれた部分をy軸周りに$ $1回転してできる立体の体積Vを求めよ.$ $接点を(t,\ log t)とする.\ また,\ y’=1x\ である.$ $接線の方程式は y=1t(x-t)+log t=1tx+log t-1$ $これが原点を通るから t=e より y=1ex 接点\ (e,\ 1)$ これが原点を通る条件を考慮して,\ 接線の方程式と接点を求める. y軸周りの回転体であるから,\ y軸に垂直な平面で切断しなければならない. {y=log xをx=e^y\ に変形してy方向に積分},\ つまり\ π∫x²dy\ を計算する. ここで,\ π∫(e^y)²dy\ で求まるのは図の赤枠部分の回転体の体積である. よって,\ 斜線部分の回転体の体積を引く必要がある.\ これは{半径e,\ 高さ1の円錐}である. y=cos x\ (0 x{π}{2}),\ x軸,\ y軸で囲まれた部分をy軸周りに1回転してできる$ $立体の体積Vを求めよ.$ y軸周りの回転体であるから,\ π∫x²dy\ を計算すればよい. しかし,\ y=cos x\ を\ x=\ の形に変換することができない. そこで,\ 逆に{dyをdxに変換}する.\ 要は{置換積分}である. 同時に{積分区間が変化}することに注意.\ 後は部分積分を2回繰り返せばよい.

