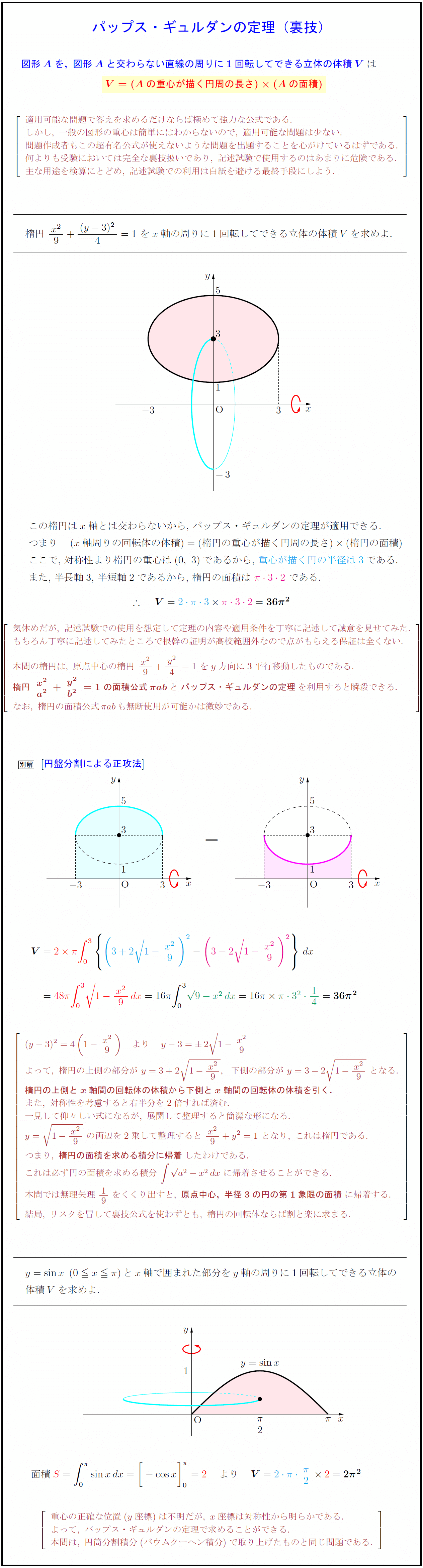
図形Aを,\ 図形Aと交わらない直線の周りに1回転してできる立体の体積Vは$ V=(Aの重心が描く円周の長さ)(Aの面積)$} 適用可能な問題で答えを求めるだけならば極めて強力な公式である. しかし,\ 一般の図形の重心は簡単にはわからないので,\ 適用可能な問題は少ない. 問題作成者もこの超有名公式が使えないような問題を出題することを心がけているはずである. 何よりも受験においては完全な裏技扱いであり,\ 記述試験で使用するのはあまりに危険である. 主な用途を検算にとどめ,\ 記述試験での利用は白紙を避ける最終手段にしよう. 楕円\ {x²}{9}+{(y-3)²}{4}=1\ をx軸の周りに1回転してできる立体の体積Vを求めよ.$ この楕円は$x$軸とは交わらないから,\ パップス・ギュルダンの定理が適用できる. つまり $(x軸周りの回転体の体積)=(楕円の重心が描く円周の長さ)(楕円の面積)$ ここで,\ 対称性より楕円の重心は$(0,\ 3)$であるから,\ 重心が描く円の半径は3}である. また,\ 半長軸3,\ 半短軸2であるから,\ 楕円の面積は\ $π32}$\ である. 気休めだが,\ 記述試験での使用を想定して定理の内容や適用条件を丁寧に記述して誠意を見せてみた. もちろん丁寧に記述してみたところで根幹の証明が高校範囲外なので点がもらえる保証は全くない. 本問の楕円は,\ 原点中心の楕円\ {x²}{9}+{y²}{4}=1\ をy方向に3平行移動したものである. {楕円\ {x²}{a²}+{y²}{b²}=1\ の面積公式π ab}と{パップス・ギュルダンの定理}を利用すると瞬殺できる. なお,\ 楕円の面積公式π abも無断使用が可能かは微妙である. よって,\ 楕円の上側の部分が\ y=3+2{1-{x²}{9,下側の部分が\ y=3-2{1-{x²}{9\ となる. {楕円の上側とx軸間の回転体の体積から下側とx軸間の回転体の体積を引く.} また,\ 対称性を考慮すると右半分を2倍すれば済む. 一見して仰々しい式になるが,\ 展開して整理すると簡潔な形になる. y={1-{x²}{9\ の両辺を2乗して整理すると\ {x²}{9}+y²=1\ となり,\ これは楕円である. つまり,\ {楕円の面積を求める積分に帰着}したわけである. これは必ず円の面積を求める積分\ ∫{a²-x²}dx\ に帰着させることができる. 本問では無理矢理\ 19\ をくくり出すと,\ {原点中心,\ 半径3の円の第1象限の面積}に帰着する. 結局,\ リスクを冒して裏技公式を使わずとも,\ 楕円の回転体ならば割と楽に求まる. $y=sin x\ (0 xπ)とx軸で囲まれた部分をy軸の周りに1回転してできる立体の$ $体積Vを求めよ.$ 重心の正確な位置(y座標)は不明だが,\ x座標は対称性から明らかである. よって,\ パップス・ギュルダンの定理で求めることができる. 本問は,\ 円筒分割積分(バウムクーヘン積分)で取り上げたものと同じ問題である.

