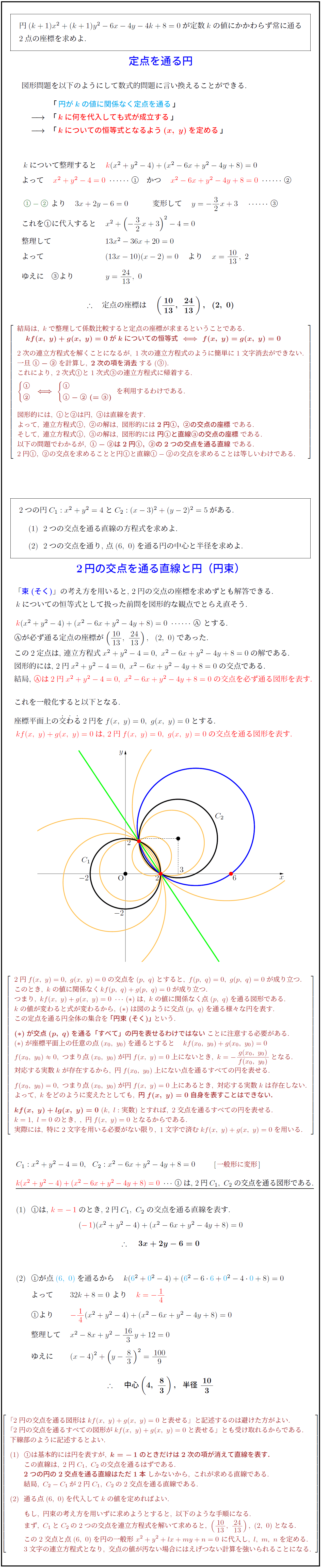
スライダーを動かして方程式がkの値によってどう変化するか確認してください。
特にk=-1とk=0のとき、そして中心原点の円は表せないことが重要です。
円$(k+1)x^2+(k+1)y^2-6x-4y-4k+8=0$が定数$k$の値にかかわらず常に通る
2点の座標を求めよ. 定点を通る円
図形問題を以下のようにして数式的問題に言い換えることができる.{円がkの値に関係なく定点を通る}\,」}$
kに何を代入しても式が成立する}\,」}$
kについての恒等式となるよう(x,\ y)を定める}\,」}$
$kについて整理すると
結局は,\ kで整理して係数比較すると定点の座標が求まるということである.
kf(x,\ y)+g(x,\ y)=0がkについての恒等式\ ⇔\ f(x,\ y)=g(x,\ y)=0}
2次の連立方程式を解くことになるが,\ 1次の連立方程式のように簡単に1文字消去ができない.
一旦①-②}を計算し,\ 2次の項を消去}する(③).
これにより,\ 2次式①と1次式③の連立方程式に帰着する.
図形的には,\ ①と②は円,\ ③は直線を表す.
よって,\ 連立方程式①,\ ②の解は,\ 図形的には2円①,\ ②の交点の座標}である.
そして,\ 連立方程式①,\ ③の解は,\ 図形的には円①と直線③の交点の座標}である.
以下の問題でわかるが,\ ①-②は2円①,\ ②の2つの交点を通る直線}である.
2円①,\ ②の交点を求めることと円①と直線①-②の交点を求めることは等しいわけである.
2つの円$C_1:x^2+y^2=4$と$C_2:(x-3)^2+(y-2)^2=5$がある.
(1)\ \ 2つの交点を通る直線の方程式を求めよ.
(2)\ \ 2つの交点を通り,\ 点$(6,\ 0)$を通る円の中心と半径を求めよ. \\
{2円の交点を通る直線と円(円束)束(そく)」の考え方を用いると,\ 2円の交点の座標を求めずとも解答できる.
$k$についての恒等式として扱った前問を図形的な観点でとらえ直そう.
$k}(x^2+y^2-4)+(x^2-6x+y^2-4y+8)=0\ ・・・・・・\,\maru{ A}$\ とする.
\maru{ A}が必ず通る定点の座標が$10}{13},\ 24}{13},\ \ (2,\ 0)$であった.
この2定点は,\ 連立方程式$x^2+y^2-4=0,\ x^2-6x+y^2-4y+8=0$の解である.
図形的には,\ 2円$x^2+y^2-4=0,\ x^2-6x+y^2-4y+8=0$の交点である.
結局,\ \maru{ A}は2円$x^2+y^2-4=0,\ x^2-6x+y^2-4y+8=0$の交点を必ず通る図形を表す.}
これを一般化すると以下となる.
座標平面上の\.{交}\.{わ}\.{る}2円を$f(x,\ y)=0,\ g(x,\ y)=0$とする.
$kf(x,\ y)+g(x,\ y)=0$は,\ 2円$f(x,\ y)=0,\ g(x,\ y)=0$の交点を通る図形を表す.} \\\
2円f(x,\ y)=0,\ g(x,\ y)=0の交点を(p,\ q)とすると,\ f(p,\ q)=0,\ g(p,\ q)=0が成り立つ.
このとき,\ kの値に関係なく\,kf(p,\ q)+g(p,\ q)=0が成り立つ.
つまり,\ kf(x,\ y)+g(x,\ y)=0\ ・・・\,(*)は,\ kの値に関係なく点(p,\ q)を通る図形である.
kの値が変わると式が変わるから,\ (*)は図のように交点(p,\ q)を通る様々な円を表す.
この定点を通る円全体の集合を「円束(そく)」}という.
(*)が交点(p,\ q)を通る「すべて」の円を表せるわけではない}ことに注意する必要がある.
(*)が座標平面上の任意の点(x_0,\ y_0)を通るとすると kf(x_0,\ y_0)+g(x_0,\ y_0)=0
f(x_0,\ y_0)≠0,\ つまり点(x_0,\ y_0)が円f(x,\ y)=0上にないとき,\ k=-g(x_0,\ y_0)}{f(x_0,\ y_0)}\,となる.
対応する実数kが存在するから,\ 円f(x_0,\ y_0)上にない点を通るすべての円を表せる.
f(x_0,\ y_0)=0,\ つまり点(x_0,\ y_0)が円f(x,\ y)=0上にあるとき,\ 対応する実数kは存在しない.
よって,\ kをどのように変えたとしても,\ 円f(x,\ y)=0自身を表すことはできない.}
kf(x,\ y)+lg(x,\ y)=0}\ (k,\ l:実数)とすれば,\ 2交点を通るすべての円を表せる.
k=1,\ l=0のとき,\ ,\ 円f(x,\ y)=0となるからである.
実際には,\ 特に2文字を用いる必要がない限り,\ 1文字で済むkf(x,\ y)+g(x,\ y)=0を用いる.
$C_1:x^2+y^2-4=0,\ \ C_2:x^2-6x+y^2-4y+8=0$ $[\,一般形に変形\,}]$} \,\ 2円$C_1,\ C_2$の交点を通る図形である. \\
(1)\ \ ①は,\ $k=-\,1}$のとき,\ 2円$C_1,\ C_2$の交点を通る直線を表す.
「2円の交点を通る図形はkf(x,\ y)+g(x,\ y)=0と表せる」と記述するのは避けた方がよい.
「2円の交点を通るすべての図形がkf(x,\ y)+g(x,\ y)=0と表せる」とも受け取れるからである.
下線部のように記述するとよい.
(1)\ \ ①は基本的には円を表すが,\ k=-\,1のときだけは2次の項が消えて直線を表す.}
\ \ この直線は,\ 2円C_1,\ C_2\,の交点を通るはずである.
\ \ 2つの円の2交点を通る直線はただ1本}しかないから,\ これが求める直線である.
\ \ 結局,\ C_2-C_1\,が2円C_1,\ C_2\,の2交点を通る直線である.
(2)\ \ 通る点(6,\ 0)を代入してkの値を定めればよい.
\ \ もし,\ 円束の考え方を用いずに求めようとすると,\ 以下のような手順になる.
\ \ まず,\ C_1\,とC_2\,の2つの交点を連立方程式を解いて求めると,\ 10}{13},\ 24}{13},\ (2,\ 0)となる.
\ \ この2交点と点(6,\ 0)を円の一般形\ x^2+y^2+lx+my+n=0\ に代入し,\ l,\ m,\ nを定める.
\ \ 3文字の連立方程式となり,\ 交点の値が汚ない場合にはえげつない計算を強いられることになる.

