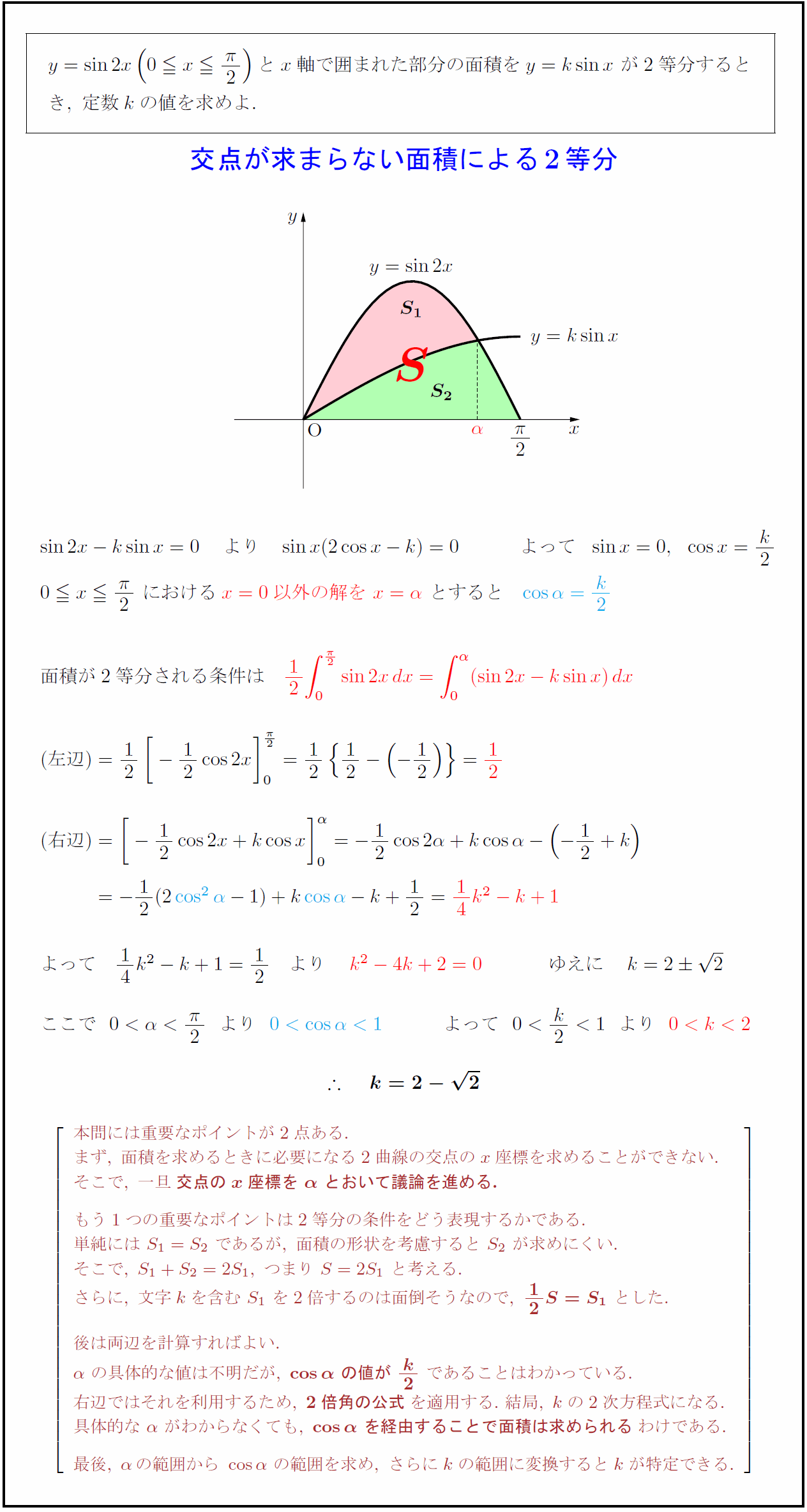
y=sin2x(0 x{π}{2})とx軸で囲まれた部分の面積をy=ksin x\ が2等分すると$ $き,\ 定数kの値を求めよ.$ $面積が2等分される条件は 本問には重要なポイントが2点ある. まず,\ 面積を求めるときに必要になる2曲線の交点のx座標を求めることができない. そこで,\ 一旦{交点のx座標を\ α\ とおいて議論を進める.} もう1つの重要なポイントは2等分の条件をどう表現するかである. 単純には\ S₁=S₂\ であるが,\ 面積の形状を考慮すると\ S₂\ が求めにくい. そこで,\ S₁+S₂=2S₁,\ つまり\ S=2S₁\ と考える. さらに,\ 文字kを含む\ S₁\ を2倍するのは面倒そうなので,\ {12S=S₁}\ とした. 後は両辺を計算すればよい. α\ の具体的な値は不明だが,\ {cosα\ の値が\ k2}\ であることはわかっている. 右辺ではそれを利用するため,\ {2倍角の公式}を適用する.\ 結局,\ kの2次方程式になる. 具体的な\ α\ がわからなくても,\ {cosα\ を経由することで面積は求められる}わけである. 最後,\ αの範囲から\ cosα\ の範囲を求め,\ さらにkの範囲に変換するとkが特定できる.

