3点$(6,\ -\,2),\ (-\,1,\ 5),\ (8,\ 2)$を頂点とする三角形の外接円の方程式を求めよ. 三角形の外接円の方程式 \\
三角形の外接円の方程式は,\ 結局は座標平面上の異なる3点を通る円の方程式である. 3点の座標から円の方程式を求める場合,\ 一般形を利用するのが基本である.
$x^2+y^2+lx+my+n=0}\ とおく.
整理すると
一般形に通る3点の座標を代入すると,\ 3文字の連立1次方程式}になる.
連立方程式の大原則は1文字消去}にある.
本問の場合,\ 最も消去しやすいnを消去するのがよいだろう.
①+②\ でnを消去}して 7l-7m=-\,14 よって l-m=-\,2
①+③\ でnを消去}して 9l-3m=-\,42 よって 3l-m=-\,14
1文字消去の原則に従い,\ 必ず同じ文字を消去する}こと.
他に消去しやすい文字があると誘惑に負けて違う文字を消去してしまう人が多いので注意してほしい.
こっちではnを消去してあっちではlを消去してなどとやっていると堂々巡りになる.
得られた2式から l=-\,6,\ m=-\,4 このとき,\ ②より n=-\,12
「円の方程式を求めよ」とあれば,\ 円の中心や半径を答える必要はなく,\ 一般形のまま答えてよい.
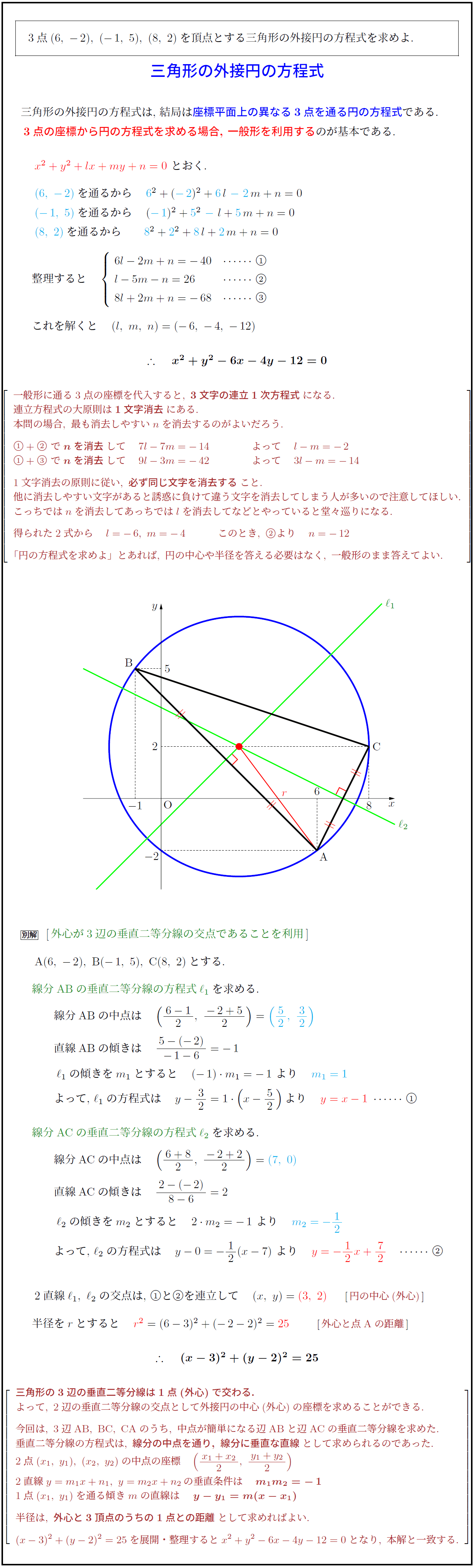
外心が3辺の垂直二等分線の交点であることを利用}\,
線分ABの垂直二等分線の方程式$ℓ_1$}を求める.
線分ABの中点は
直線ABの傾きは
$ℓ_1$の傾きを$m_1$とすると
線分ACの垂直二等分線の方程式$ℓ_2$}を求める.
半径を$r$とすると外心と点A}の距離}\
三角形の3辺の垂直二等分線は1点(外心)で交わる.}
よって,\ 2辺の垂直二等分線の交点として外接円の中心(外心)の座標を求めることができる.
今回は,\ 3辺AB,\ BC,\ CAのうち,\ 中点が簡単になる辺ABと辺ACの垂直二等分線を求めた.}
垂直二等分線の方程式は,\ 線分の中点を通り,\ 線分に垂直な直線}として求められるのであった.
2点(x_1,\ y_1),\ (x_2,\ y_2)の中点の座標 x_1+x_2}{2},\ y_1+y_2}{2}
2直線y=m_1x+n_1,\ y=m_2x+n_2\,の垂直条件は m_1m_2=-\,1}
1点(x_1,\ y_1)を通る傾きmの直線は \ y-y_1=m(x-x_1)}
半径は,\ 外心と3頂点のうちの1点との距離}として求めればよい.
(x-3)^2+(y-2)^2=25を展開・整理するとx^2+y^2-6x-4y-12=0となり,\ 本解と一致する.

