円$x^2+y^2=1$上の点Pと2点A$(3,\ 0)$,\ B$(0,\ 2)$でできる$△$PABの面積の最大値と
最小値を求めよ. 円周上の点と直線の最長距離と最短距離}
線分ABの長さは $√{(0-3)^2+(2-0)^2}=√{13}$
2点A$(3,\ 0)$,\ B$(0,\ 2)$を通る直線の方程式は $2x+3y-6=0$
円の中心(0,\ 0)と直線$2x+3y-6=0$の距離は
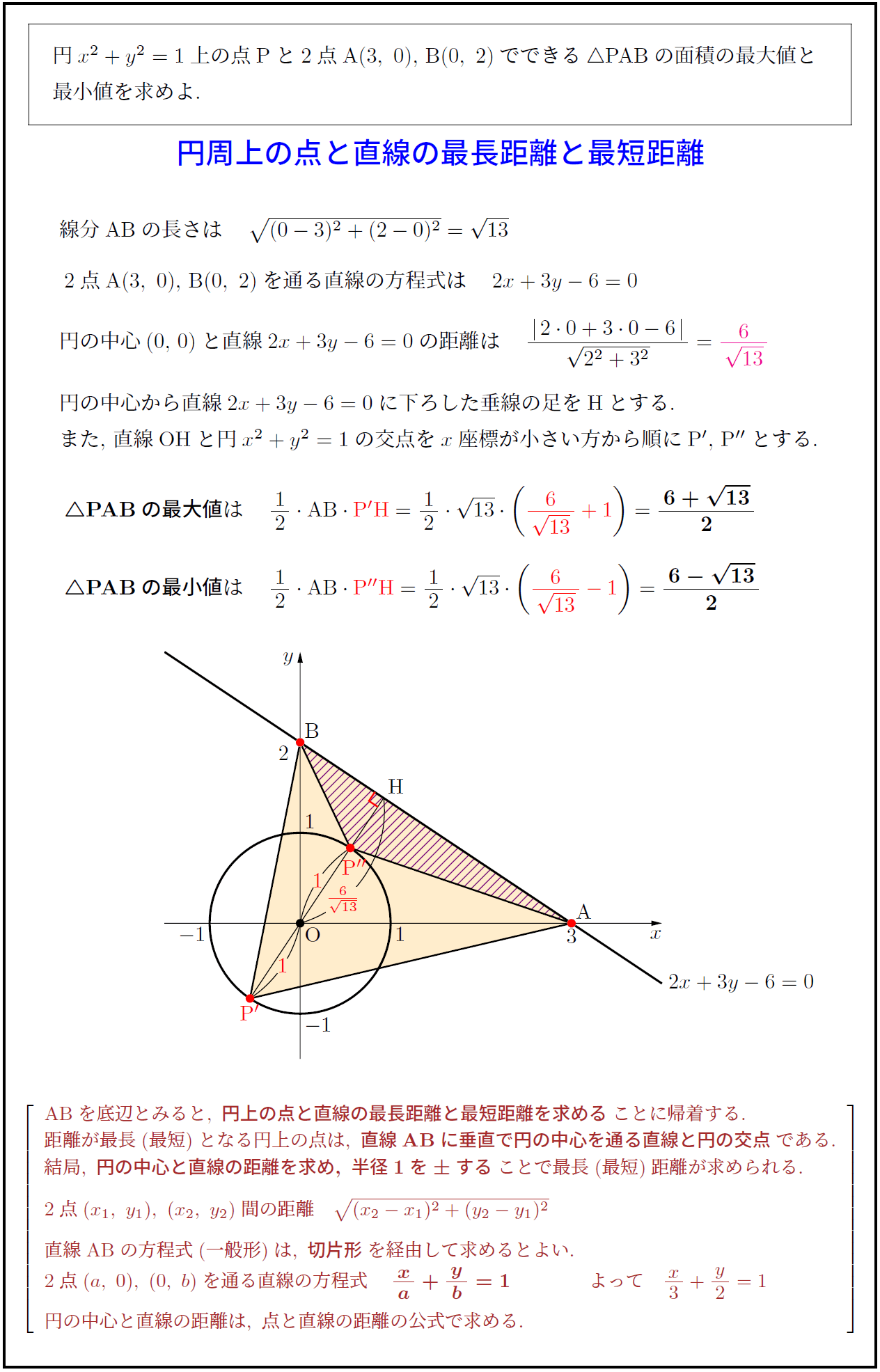
円の中心から直線$2x+3y-6=0$に下ろした垂線の足をHとする.
また,\ 直線OHと円$x^2+y^2=1$の交点を$x$座標が小さい方から順にP$’$,\ P$”$とする.
$△}$PABの最大値}は
AB}を底辺とみると,\ 円上の点と直線の最長距離と最短距離を求める}ことに帰着する.
距離が最長(最短)となる円上の点は,\ 直線AB}に垂直で円の中心を通る直線と円の交点}である.
結局,\ 円の中心と直線の距離を求め,\ 半径1を ± する}ことで最長(最短)距離が求められる.
2点(x_1,\ y_1),\ (x_2,\ y_2)間の距離 √{(x_2-x_1)^2+(y_2-y_1)^2}
直線AB}の方程式(一般形)は,\ 切片形}を経由して求めるとよい.
2点(a,\ 0),\ (0,\ b)を通る直線の方程式 xa+ yb=1} よって x3+ y2=1
円の中心と直線の距離は,\ 点と直線の距離の公式で求める.

