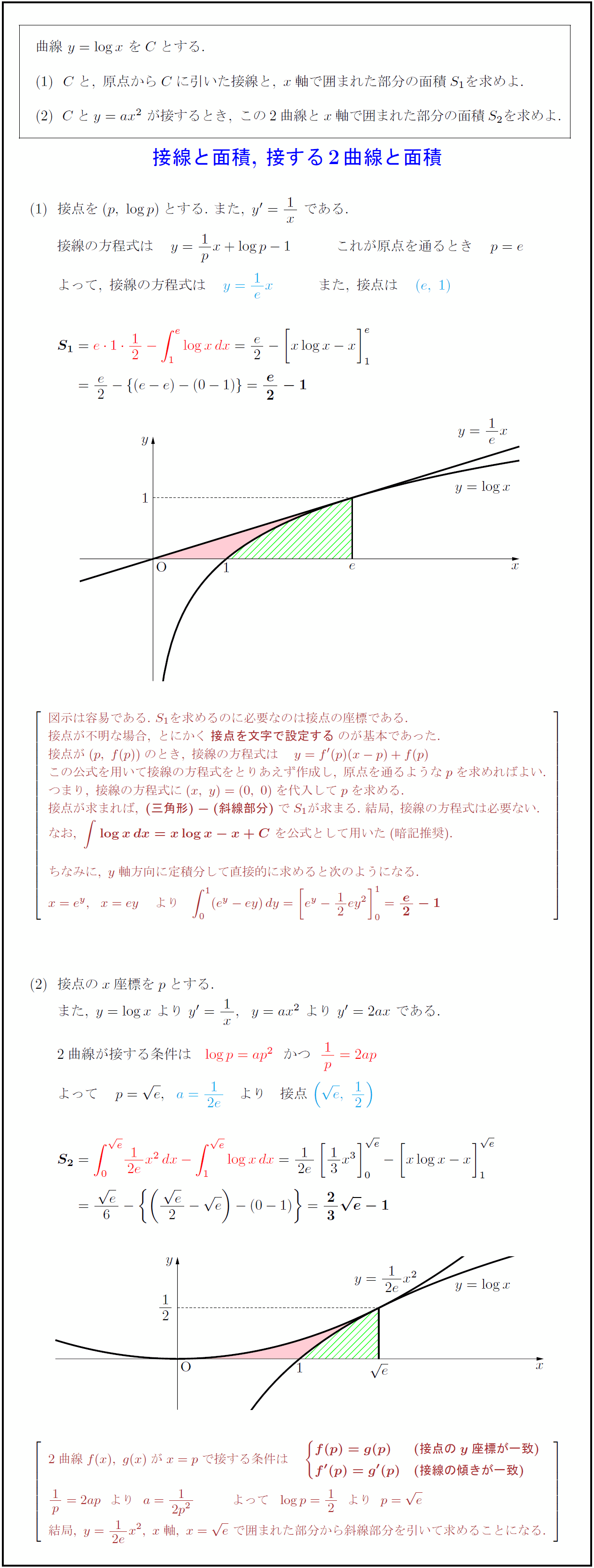
曲線\ y=log x\ をCとする.$ $Cと,\ 原点からCに引いた接線と,\ x軸で囲まれた部分の面積S₁を求めよ.$ $Cとy=ax²\ が接するとき,\ この2曲線とx軸で囲まれた部分の面積S₂を求めよ.$ $接点を(p,\ log p)とする.\ また,\ y’=1x\ である.$ $接線の方程式は y=1px+log p-1 これが原点を通るとき p=e$ 図示は容易である.\ S₁を求めるのに必要なのは接点の座標である. 接点が不明な場合,\ とにかく{接点を文字で設定する}のが基本であった. 接点が(p,\ f(p))のとき,\ 接線の方程式は y=f'(p)(x-p)+f(p) この公式を用いて接線の方程式をとりあえず作成し,\ 原点を通るようなpを求めればよい. つまり,\ 接線の方程式に(x,\ y)=(0,\ 0)を代入してpを求める. 接点が求まれば,\ {(三角形)-(斜線部分)}でS₁が求まる.\ 結局,\ 接線の方程式は必要ない. なお,\ {∫log xdx=xlog x-x+C}\ を公式として用いた(暗記推奨). ちなみに,\ y軸方向に定積分して直接的に求めると次のようになる. x=e^y,x=ey より ∫(e^y-ey)dy=[e^y-12ey²}{0}{1}={ e2-1} 接点のx座標をpとする.$ 2曲線f(x),\ g(x)がx=pで接する条件は { f(p)=g(p) (接点のy座標が一致) f'(p)=g'(p) (接線の傾きが一致) } [-.5zh] 1p=2apよりa={1}{2p²} よってlog p=12よりp= e 結局,\ y={1}{2e}x²,\ x軸,\ x= e\ で囲まれた部分から斜線部分を引いて求めることになる.

