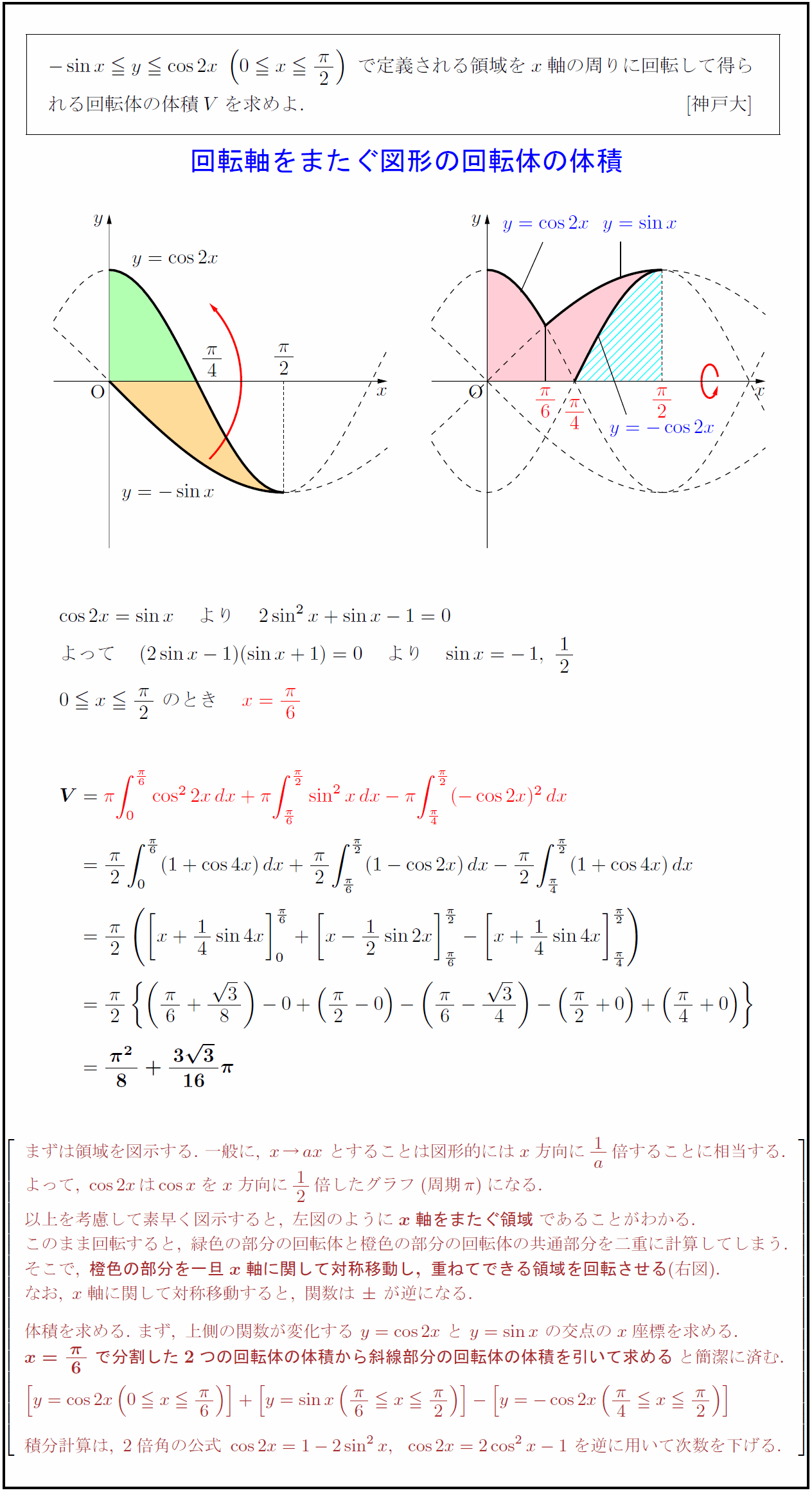
-sin x ycos2x\ (0 x{π}{2})\ で定義される領域をx軸の周りに回転して得ら$ $れる回転体の体積Vを求めよ. [神戸大]$ 回転軸をまたぐ図形の回転体の体積 まずは領域を図示する.\ 一般に,\ x→ax\ とすることは図形的にはx方向に1a倍することに相当する. よって,\ cos2xはcos xをx方向に12倍したグラフ(周期π)になる. 以上を考慮して素早く図示すると,\ 左図のように{x軸をまたぐ領域}であることがわかる. このまま回転すると,\ 緑色の部分の回転体と橙色の部分の回転体の共通部分を二重に計算してしまう. そこで,\ {橙色の部分を一旦x軸に関して対称移動し,\ 重ねてできる領域を回転させる}(右図). なお,\ x軸に関して対称移動すると,\ 関数はが逆になる. 体積を求める.\ まず,\ 上側の関数が変化する\ y=cos2x\ と\ y=sin x\ の交点のx座標を求める. {x={π}{6}\ で分割した2つの回転体の体積から斜線部分の回転体の体積を引いて求める}と簡潔に済む. 積分計算は,\ 2倍角の公式\ cos2x=1-2sin²x,cos2x=2cos²x-1\ を逆に用いて次数を下げる.

