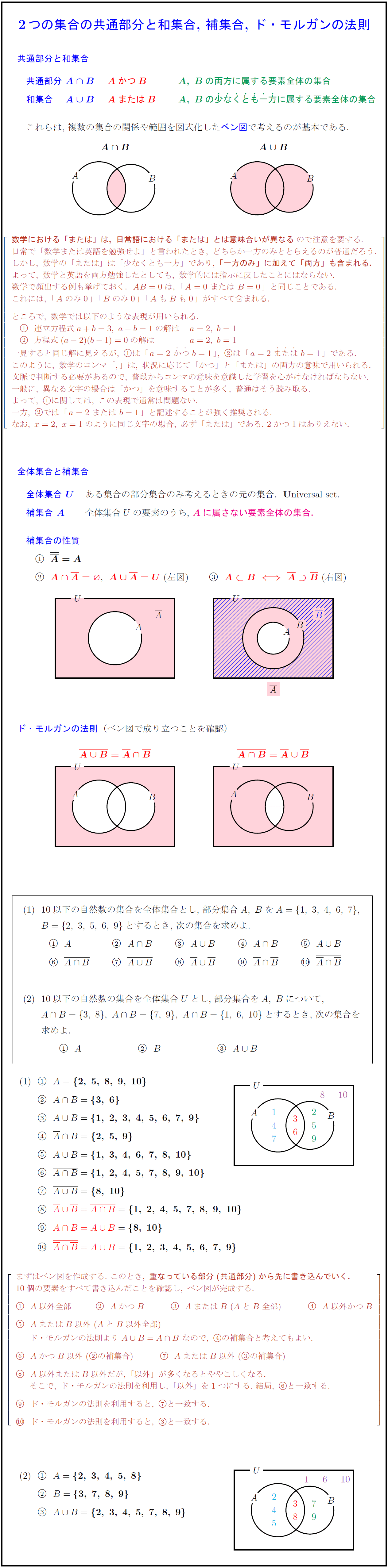
2つの集合の共通部分と和集合,\ 補集合,\ ド・モルガンの法則 共通部分と和集合 共通部分\ ${A B}$ ${AかつB$ ${A,\ Bの両方に属する要素全体の集合$ 和集合 \ ${A B}$ ${AまたはB$ ${A,\ Bの少}な}く}と}も}一}方}に属する要素全体の集合$ これらは,\ 複数の集合の関係や範囲を図式化したベン図で考えるのが基本である. {数学における「または」は,\ 日常語における「または」とは意味合いが異なる}ので注意を要する. 日常で「数学または英語を勉強せよ」と言われたとき,\ どちらか一方のみととらえるのが普通だろう. しかし,\ 数学の「または」は「少なくとも一方」であり,\ {「一方のみ」に加えて「両方」も含まれる.} よって,\ 数学と英語を両方勉強したとしても,\ 数学的には指示に反したことにはならない. 数学で頻出する例も挙げておく.AB=0は,\ 「A=0\ または\ B=0」と同じことである. これには,\ 「Aのみ0」「Bのみ0」「AもBも0」がすべて含まれる. ところで,\ 数学では以下のような表現が用いられる. 連立方程式a+b=3,\ a-b=1の解は a=2,\ b=1 方程式(a-2)(b-1)=0の解は \ a=2,\ b=1 一見すると同じ解に見えるが,\ は「a=2\ か}つ}\ b=1」,\ は「a=2\ ま}た}は}\ b=1」である. このように,\ 数学のコンマ「,」は,\ 状況に応じて「かつ」と「または」の両方の意味で用いられる. 文脈で判断する必要があるので,\ 普段からコンマの意味を意識した学習を心がけなければならない. 一般に,\ 異なる文字の場合は「かつ」を意味することが多く,\ 普通はそう読み取る. よって,\ に関しては,\ この表現で通常は問題ない. 一方,\ では「a=2\ または\ b=1」と記述することが強く推奨される. なお,\ x=2,\ x=1のように同じ文字の場合,\ 必ず「または」である.\ 2かつ1はありえない. 全体集合と補集合 全体集合\ ${U}$ ある集合の部分集合のみ考えるときの元の集合.U}niversal set. 補集合\ ${ A}$ 全体集合$U$の要素のうち,\ ${A}$に属さない要素全体の集合. 補集合の性質}{ド・モルガンの法則(ベン図で成り立つことを確認)\ 10以下の自然数の集合を全体集合とし,\ 部分集合$A,\ B$を$A={1,\ 3,\ 4,\ 6,\ 7}$, $B={2,\ 3,\ 5,\ 6,\ 9}$とするとき,\ 次の集合を求めよ. 10以下の自然数の集合を全体集合$U$とし,\ $部分集合をA,\ B$について, $A B={3,\ 8},\ A B={7,\ 9},\ A B={1,\ 6,\ 10}$とするとき,\ 次の集合を 求めよ. まずはベン図を作成する.\ このとき,\ {重なっている部分(共通部分)から先に書き込んでいく.} 10個の要素をすべて書き込んだことを確認し,\ ベン図が完成する. A以外全部 AかつB AまたはB\ (AとB全部) A以外かつB AまたはB以外\ (AとB以外全部) ド・モルガンの法則より\ A B= A B}\ なので,\ の補集合と考えてもよい. ⑥AかつB以外\ (の補集合) ⑦AまたはB以外\ (の補集合) ⑧A以外またはB以外だが,\ 「以外」が多くなるとややこしくなる. そこで,\ ド・モルガンの法則を利用し,\ 「以外」を1つにする.\ 結局,\ ⑥と一致する. ⑨ド・モルガンの法則を利用すると,\ ⑦と一致する. \maru{10}ド・モルガンの法則を利用すると,\ と一致する.

