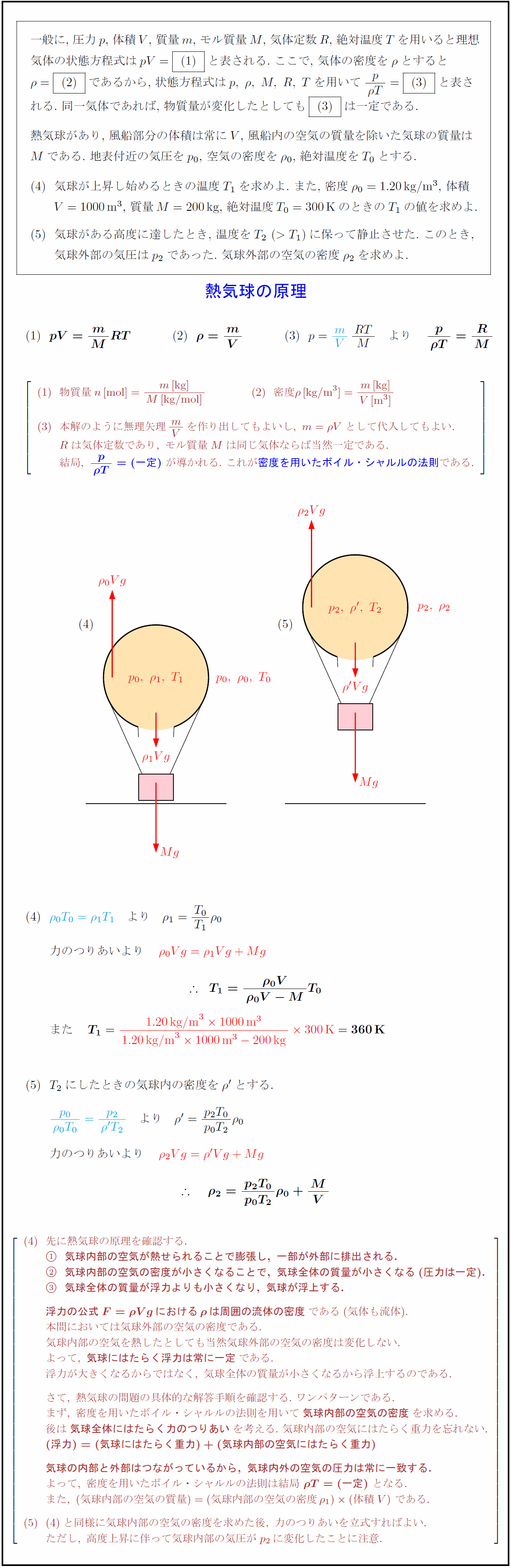
一般に, 圧力p, 体積V, 質量m, モル質量M, 気体定数R, 絶対温度Tを用いると理想
気体の状態方程式は pV= m/M·RT と表される. ここで, 気体の密度をρとすると
ρ= m/V であるから, 状態方程式は p, ρ, M, R, T を用いて p/(ρT)= R/M と表さ
れる. 同一気体であれば, 物質量が変化したとしても R/M は一定である.
熱気球があり, 風船部分の体積は常にV, 風船内の空気の質量を除いた気球の質量は
Mである. 地表付近の気圧をp₀, 空気の密度をρ₀, 絶対温度をT₀とする.
(4) 気球が上昇し始めるときの温度T₁を求めよ. また, 密度ρ₀=1.20 kg/m³, 体積
V=1000 m³, 質量M=200 kg, 絶対温度T₀=300 K のときの T₁ の値を求めよ.
(5) 気球がある高度に達したとき, 温度をT₂ (>T₁) に保って静止させた. このとき,
気球外部の気圧は p₂ であった. 気球外部の空気の密度 ρ₂ を求めよ.
━━━━━━━━━━━━━━━━━━━━━━━━━━
熱気球の原理
━━━━━━━━━━━━━━━━━━━━━━━━━━
(1) pV= m/M·RT
(2) ρ= m/V
(3) p= (m/V)·(RT/M) より p/(ρT)= R/M
〔
(1) 物質量 n[mol]= m[kg]/M[kg/mol]
(2) 密度 ρ[kg/m³]= m[kg]/V[m³]
(3) 本解のように無理矢理 m/V を作り出してもよいし, m=ρV として代入してもよい.
Rは気体定数であり, モル質量Mは同じ気体ならば当然一定である.
結局, p/(ρT)=一定 が導かれる. これが 密度を用いたボイル・シャルルの法則 である.
〕
(4) ρ₀T₀=ρ₁T₁ より ρ₁= (T₀/T₁) ρ₀
力のつりあいより ρ₀Vg=ρ₁Vg+Mg
∴ T₁= (ρ₀V)/(ρ₀V−M) · T₀
また T₁= (1.20 kg/m³ × 1000 m³)/(1.20 kg/m³ × 1000 m³ − 200 kg) × 300 K
= 360 K
(5) T₂ にしたときの気球内の密度を ρ′ とする.
p₀/(ρ₀T₀)= p₂/(ρ′T₂) より ρ′= (p₂T₀)/(p₀T₂) ρ₀
力のつりあいより ρ₂Vg=ρ′Vg+Mg
∴ ρ₂= (p₂T₀)/(p₀T₂) ρ₀ + M/V
〔
(4) 先に熱気球の原理を確認する.
① 気球内部の空気が熱せられることで膨張し, 一部が外部に排出される.
② 気球内部の空気の密度が小さくなることで, 気球全体の質量が小さくなる (圧力は一定).
③ 気球全体の質量が浮力よりも小さくなり, 気球が浮上する.
浮力の公式 F=ρVg における ρ は周囲の流体の密度である (気体も流体).
本問においては気球外部の空気の密度である.
気球内部の空気を熱したとしても当然気球外部の空気の密度は変化しない.
よって, 気球にはたらく浮力は常に一定である.
浮力が大きくなるからではなく, 気球全体の質量が小さくなるから浮上するのである.
さて, 熱気球の問題の具体的な解答手順を確認する. ワンパターンである.
まず, 密度を用いたボイル・シャルルの法則を用いて 気球内部の空気の密度 を求める.
後は 気球全体にはたらく力のつりあい を考える. 気球内部の空気にはたらく重力を忘れない.
(浮力)=(気球にはたらく重力)+(気球内部の空気にはたらく重力)
気球の内部と外部はつながっているから, 気球内外の空気の圧力は常に一致する.
よって, 密度を用いたボイル・シャルルの法則は結局 ρT=一定 となる.
また, (気球内部の空気の質量)=(気球内部の空気の密度 ρ₁)×(体積V) である.
(5) (4)と同様に気球内部の空気の密度を求めた後, 力のつりあいを立式すればよい.
ただし, 高度上昇に伴って気球内部の気圧が p₂ に変化したことに注意.
〕

