気体の状態変化
気体の状態変化は, 熱力学分野における最重要事項である. 大きく4パターンに分類される.
どの変化にせよ, ①ボイル・シャルルの法則と②熱力学第一法則を用いて解くしかない.
実際の問題は次項から扱うので, 本項では各変化ごとに以下がどうなるかをまとめておく.
{
① ボイル・シャルルの法則 pV/T = (一定)
② 熱力学第一法則 Q_in = ΔU + W_out
③ その変化特有の関係
}
(図要素:V₁, V₂, ΔV, 温度の高低, W_out の領域表示など/TeX コマンド除去により図は消滅)
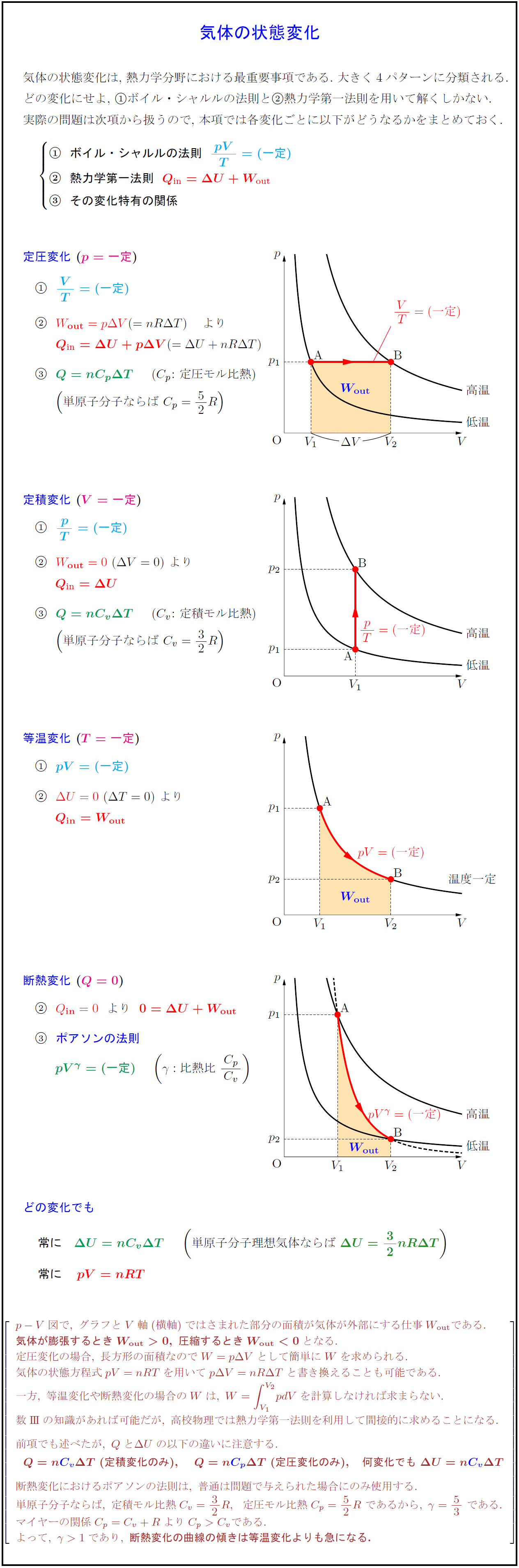
定圧変化 (p = 一定)
① VT = (一定)
② W_out = pΔV (= nRΔT) より
Q_in = ΔU + pΔV (= ΔU + nRΔT)
③ Q = nC_pΔT (C_p:定圧モル比熱)
(単原子分子ならば C_p = 5/2 R)
(図要素:p₁→p₂ の縦移動, “pT=(一定)” の位置表示など)
定積変化 (V = 一定)
① pT = (一定)
② W_out = 0 (ΔV = 0) より
Q_in = ΔU
③ Q = nC_vΔT (C_v:定積モル比熱)
(単原子分子ならば C_v = 3/2 R)
(図要素:pV=(一定), W_out の陰影領域, 温度一定の線など)
等温変化 (T = 一定)
① pV = (一定)
② ΔU = 0 (ΔT = 0) より
Q_in = W_out
断熱変化 (Q = 0)
② Q_in = 0 より 0 = ΔU + W_out
③ ポアソンの法則
pV^γ = (一定) (γ: 比熱比 C_p / C_v)
どの変化でも
常に ΔU = nC_vΔT (単原子分子理想気体ならば ΔU = 3/2 nRΔT)
常に pV = nRT
[補足]
p-V図で, グラフとV軸(横軸)ではさまれた部分の面積が気体が外部にする仕事W_outである.
気体が膨張するときW_out>0, 圧縮するときW_out<0となる.
定圧変化の場合, 長方形の面積なのでW = pΔVとして簡単にWを求められる.
気体の状態方程式pV = nRTを用いてpΔV = nRΔTと書き換えることも可能である.
一方, 等温変化や断熱変化の場合のWは, W = ∫(V₁→V₂) p dV を計算しなければ求まらない.
数学IIIの知識があれば可能だが, 高校物理では熱力学第一法則を利用して間接的に求めることになる.
前項でも述べたが, QとΔUの違いに注意する.
Q = nC_vΔT (定積変化のみ)
Q = nC_pΔT (定圧変化のみ)
何変化でも ΔU = nC_vΔT
断熱変化におけるポアソンの法則は, 普通は問題で与えられた場合にのみ使用する.
単原子分子ならば, 定積モル比熱C_v = 3/2 R, 定圧モル比熱C_p = 5/2 R であるから, γ = 5/3 である.
マイヤーの関係 C_p = C_v + R より C_p > C_v である.
よって, γ > 1であり, 断熱変化の曲線の傾きは等温変化よりも急になる.

