
2019年、天下の京都大学が文系の第1問の問2にて小学生レベルの問題を出題してきた。
京大受験生も舐められたものである。文系など所詮はそのレヴェルということなのか。

8.94や18という数字が何となく意味ありげだがはて???
とりあえず解答を示す。
指導者「ふっ、小学生でも解けるぜ(`・ω・´)」

受験生「いやいやいやいや・・・・・・・・・・・・・・・」
指導者「ん?何か問題でも?」
受験生「その解答は試験時間を考慮すると非現実的です。」
指導者「え~~~必死に計算したのに~~~ヽ(`Д´)ノ」
受験生「常用対数を利用すると楽に概算できます。」
指導者「ほう・・・・・・」
受験生「log₁₀8.9418=18log₁₀(2・3・149/100) って、あれれ???」
受験生「いつものようにlog₁₀2とlog₁₀3の近似値が問題で与えられていない?」
指導者「|*`艸´)クックック・・・・・・」
実は、この年の問題冊子の表紙には例年にはなかった一文が追加されていた。
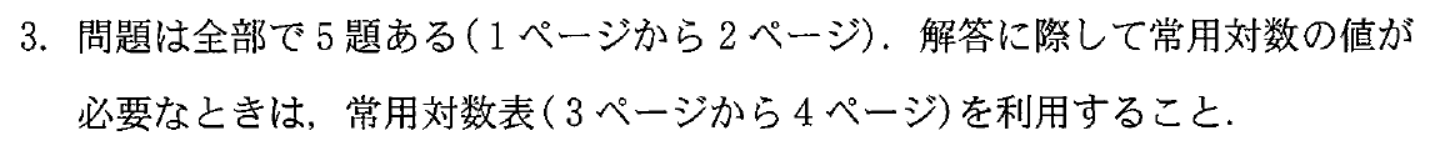
また、例年は最終問題の下部に「問題はこのページで終わりである。」との記述があるが、この年は以下のような記述になっていた。

そう、一見すると京大受験生ならば誰でも解けそうな超有名パターン問題なのだが、通常とは異なりlog₁₀2やlog₁₀3の近似値が与えられておらず、常用対数表を利用しなければならないという大学受験では極めて稀な出題だったのである。


問題を見た瞬間は楽勝だと思った京大受験生が一転して大ピンチに陥る。
常用対数表の見方がわからない。。。
常用対数表は常用対数を一番最初に学習したときに軽く触れたかもしれないが、それ以降は高校数学・受験数学において利用する機会はほぼないに等しく、見方を覚えている受験生は少ないだろう。
それでも、左上は0、右下は1に近づく全体の数値の傾向や、log₁₀2≒0.3010(おっさん冷凍)やlog₁₀3≒0.4771(死なない)などよく知られた近似値を元に一番上の行が小数第2位であることが推測できる。
ということで、標準的な解答を示すと以下のようになる。ここで、常用対数表の値は小数第5位を四捨五入した近似値なので安易にlog₁₀8.94=0.9513としてはならず、不等式で評価しなければならないことに注意する。

そういえば「8.94、18」って・・・・・・あっ!
白紙、嫌!!!
これが京大からの伝説のメッセージだ!
理系のほうでも常用対数表を利用する出題があった。こちらはラストの第6問であった。

ド・モアブルの定理(複素数平面)を利用するのが標準解答であろう。

出題意図
なぜ京都大学は常用対数表を利用する問題を出題したのだろうか。
2021年から大学入学共通テスト、2022年から新課程が始まることと無関係ではあるまい。今後は学校教育において表の読み取りを元に思考する能力や数学史を重視していくという大きな流れがあり、京大の出題はこの流れに先んじたものであったと言える。
また、高校数学で対数を学習し終えた多くの人は、以下のように認識している節がある。
「桁の大きい数の掛け算は対数を使えば楽になる」
その通りといえばその通りだが、重大な認識不足があるように思われる。
対数を利用した掛け算の原理を改めて確認しよう。
例えば、128×32を計算するとき、2の累乗数であることを利用できる。
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 210 | 211 | 212 |
| 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 | 2048 | 4096 |
このとき、128=27、32=25 を利用すると、27×25=27+5=212 となるから、表から 128×32=212=4096 とわかる。
対数はこれの表記を変えただけで、本質的には同じである。
log2(128×32)=log2(27×25)=log227+log225=7+5=12
このように、128×32 という面倒な掛け算が 7+5=12 という糞簡単な足し算に帰着する。
うおおお、対数スゲー!!!
と一瞬思うが、冷静に考えると
表がないと余計面倒やんけ!!!
という現実に気付く。
そう、対数の概念や計算法則を知っているというだけで掛け算が楽になることはない。
元の数とその対数の値を換算する「対数表」という現物が存在して初めて楽に掛け算を行えるようになるのである。
京都大学の問題は、計算機が発達した現代の我々が忘れかけていた対数「表」の恩恵を思い起こさせてくれる。いかに対数の知識を持っていようとも、常用対数表が与えられていなければその知識を役立てることができず、一番最初に示したような計算をする羽目になっていたのだ(まあ、桁数や上2桁だけならば概算でよいがそれでも面倒)。
対数表がなぜ、そしてどのように誕生したのか、以下で過去の偉大な先駆者達の足跡を辿ることにしよう。
魂が揺さぶられるような人間ドラマがそこにはある。
対数の歴史
10進法の導入
人類が常用対数表の作成に至るまでには、いくつかの大きな飛躍が必要であった。
1つ目は10進法の導入である。常用対数の底が10なのは10進法を前提としているからである。
アジアではかなり古くから10進法が浸透していたが、ヨーロッパは10進法に馴染みが薄い社会であった。実際、日本人は「八、九、十、十一、十二、・・・」と数えるが、英語(ゲルマン形言語)では「ten、eleven、twelve、thirteen、fourteen、・・・」と数えるわけで、ここには12進法の名残が見られるし、フランス語の数え方には20進法の名残が見られる。
10進法はインド・アラビアで作られ、12世紀頃からヨーロッパにも輸入されて科学者や技術者の間では有用性が認識されるようになってきてはいたが、貨幣制度と度量衡(長さ・容積・質量の計量単位)がその普及を遅らせた。貨幣制度や度量衡の変更は経済的・社会的に甚大な影響をもたらすものであり、強大な権力によってのみ成し得る。ヨーロッパで初めて度量衡が10進法に変更され、10進法が日常にまで浸透したのは、フランス革命(1789-1795)の後のことである。
シモン・ステヴィンによる10進小数の導入

Public domain, via Wikimedia Commons
シモン・ステヴィン(オランダ;1548-1620)は、近代科学のパイオニアの一人である。多くがオランダ語で発表されたこともあって国際的な知名度は今一つであるが、その業績は多岐にわたる。
物理学では、ガリレオ・ガリレイに先んじた落下の法則の発見、パスカルに先んじた静水圧のパラドックスの発見、力の平行四辺形の法則の発見、てこの原理の証明、月の引力による潮の満ち引きの説明、音楽ではヨーロッパで初めて十二平均律を算出した。
多くの業績の中でも特筆されるべきが、数学における10進小数の導入である。
商業が発達した14~15世紀の中性ヨーロッパにおいては、古代ギリシャの論理を重視する数学とは異なり、利益配分、貨幣換算、利子計算など実用性のある商業数学が発展していた。金銭を扱う商業数学においては整数と分数があれば十分で、小数への欲求は起こらなかった。
分数と小数は、観念的には以下のような点において別物である。
分数は次のように離散的で、どちらかといえば整数に近い数である。
・・・・・・、1、5/4、6/4、7/4、2、・・・・・・
もしこの間を埋めようとすれば、以下のようにより分母が大きい分数を持ち出さざるを得ない。
・・・・・・、1、17/16、9/8、19/16、5/4、・・・・・・
一方で、小数は連続的であり、無理数や誤差が生じる観測量であっても桁を増やすだけで必要な精度で近似することが可能である。
√2 ≒ 1.4、1.41、1.414、1.4142、・・・・・・
ここでは、桁を増やすと実際の値に限りなく近づいていくという極限概念が暗黙の内に仮定されており、数直線上にすき間はなくすべての点が数と1対1で対応するという現在の実数概念にも通ずるものといえる。
シモン・ステヴィンは、『十進法』(1585)の中で、小数の表記法を考案しただけでなく、整数も分数も小数も対等な扱いで1つの実数というカテゴリーに包摂し、その演算規則を確立した。ただし、ステヴィンの小数表現は現在のように小数点を用いるものではなく、19.876を「19876」のように表すものであった。
今日通貨や度量衡の単位には十進法が採用されているが、日常での利用をはじめて提唱したのはステヴィンである。実際に導入されたのはフランス革命以降であったから、時代を200年先んじていたことになる。
対数の誕生
15世紀半ばから始まった大航海時代、航海士達には高い精度の天体観測と複雑で膨大な数値計算を正確に行うことが要求された。赤道上では経度1°のずれが100kmのズレになるなど、観測誤差や計算ミスは死を意味する。また、当時最大の天体観測者であったティコ・ブラーエ(1546-1601;デンマーク)の天体観測の精度はすでに有効数字7桁に達しており、天文学においても膨大な数値計算が創造的な活動の妨げになっていた。
計算を楽にするための無数の機械的道具が発明されたが、最も重要なブレークスルーは概念的なものであった。
16世紀、航海士や天文学者を救うべく1人の男が立ち上がった。その名は
ジョン・ネイピア(1550-1617)
Samuel Freeman, Public domain, via Wikimedia Commons
スコットランドの首都エディンバラにあるマーチストン城で生を受け、八代目の城主となることが約束されていたネイピアは、非凡な才能に加えて優れた公共精神の持ち主であり、様々な発明によって多くの地域の問題を解決した。
様々な発明の中で後世にまで大きな影響を与えたのは、対数の発明であった。
ネイピアは、1594年に対数の概念に到達したとされる。しかし、概念だけで数値計算が簡単になることはなく、対数表の作成が必須である。
対数表の作成には膨大な数値計算を要するが、たった一度作成すればよい。誰かが自分の人生を犠牲にしてたった一度対数表を作成してくれさえすれば、後世の人間は計算地獄から解放されるのである。
ネイピアはすでに44歳になっていたが、その使命を自ら引き受けた。
後世のために残りの我が人生を計算に捧げよう。
ネイピア対数は現在の対数とは異なり、当時よく利用されていた三角関数の計算の簡略化を目的としていた。
たった1人での孤独な戦いが始まる。
彼が自ら落ちたのは、多くの人の想像を遙かに遙かに遙かに超える計算地獄であった。
計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算計算
恐るべき忍耐を要する果てしなく長い戦いの末、ネイピアは0°から90°までの角度1分刻みでの正弦の対数表(7桁)の作成というとてつもない偉業を成し遂げた。
対数表の完成までに要した歳月、実に
20年
1614年にラテン語で出版された『素晴らしい対数表の解説(1616年英語版:Description of the Wonderful Canon of Logarithms)』は、説明57ページに対し、対数表は90ページにも及んだ。
タイトルにもある対数の「Logarithms」は、ギリシャ語の「Logos(神の言葉)」と「Arithmons(数)」を組み合わせたネイピアの造語である。

John Napier, Public domain, via Wikimedia Commons
少しだけこの表を解説しておくと、現代の表記では左上が10000000sin34.5°の値、その右がlog0.9999999(sin34.5°)の値である(角度は60進法なので34°30’=34.5°)。10000000が掛けられているのは、当時まだ一般的ではなかった小数を避けるためである。また、logの底が0.9999999なのは、例えば底を2にするとその累乗は値が飛び飛びすぎて実用性を欠くので、できるだけ底を1に近くすることを考えてのことである。
常用対数の誕生
ネイピア対数に感銘を受けたのは、ロンドンのグレシャム大学天文学講師のヘンリー・ブリッグス(1556-1630)である。天体食の計算や航海術に関する数表も出版していたブリッグスは、膨大な算術計算や三角法の計算に忙殺されていた。1615年夏、ブリッグスはネイピアに会うためにはるばるスコットランドへ出かけていった。
ただ、単に感動を伝えるためだけに数日かけて会いに行ったわけではなかった。
ネイピア対数には実用上大きな問題点が2つあった。1の対数が0でないために掛け算や割り算に対する計算が面倒になること、真数が10倍されるときに足す数が23025842のような複雑な値になることである。
ブリッグスの真の目的は、ネイピア対数の問題点を克服し、新たな対数表を作成することにあった。ネイピアと感動の対面を果たしたブリッグスは、20年かけて対数表を作り上げたネイピアに対して心苦しさを感じつつも、覚悟を決めて提言する。
実は、ネイピア自身も途中で問題があることに気付いていた。しかし、人生の残り時間を考えると一度決めた道を突き進む他なかったのである。
ブリッグスの熱い思いを受け止め、ネイピアは決断する。
「共に新しい対数表を作ろう。」
ブリッグスがロンドンに戻った後、二人は手紙でネイピア対数の改良を巡って議論を交わしていく。1616年、その議論の中で底を10とする常用対数のアイディアに到達した。二人は再会したが、ネイピアは自分に残された時間が少ないことを悟っていた。常用対数表の作成を託されたブリッグスは、1年後に常用対数表を作成して戻ってくることを約束した。
ブリッグスは約束通り、1年間で1から1000までの数に対する14桁という超高精度の常用対数表を作り上げた。これが現在高校数学の教科書に載っている常用対数表の原型である。

Henry Briggs, Public domain, via Wikimedia Commons
ここで、log₁₀2を例に、ブリッグスが行った計算方法を現代風に少しアレンジしたものを紹介する。
まず、いわゆる開平法を用いて10の平方根、さらにその平方根を繰り返し求めていく。開平法は同様の手順を繰り返すだけでいくらでも精度が高くなるが、繰り返すほど計算が大変になる。小数点以下32桁まで求める開平法1回分の計算を示しておく。
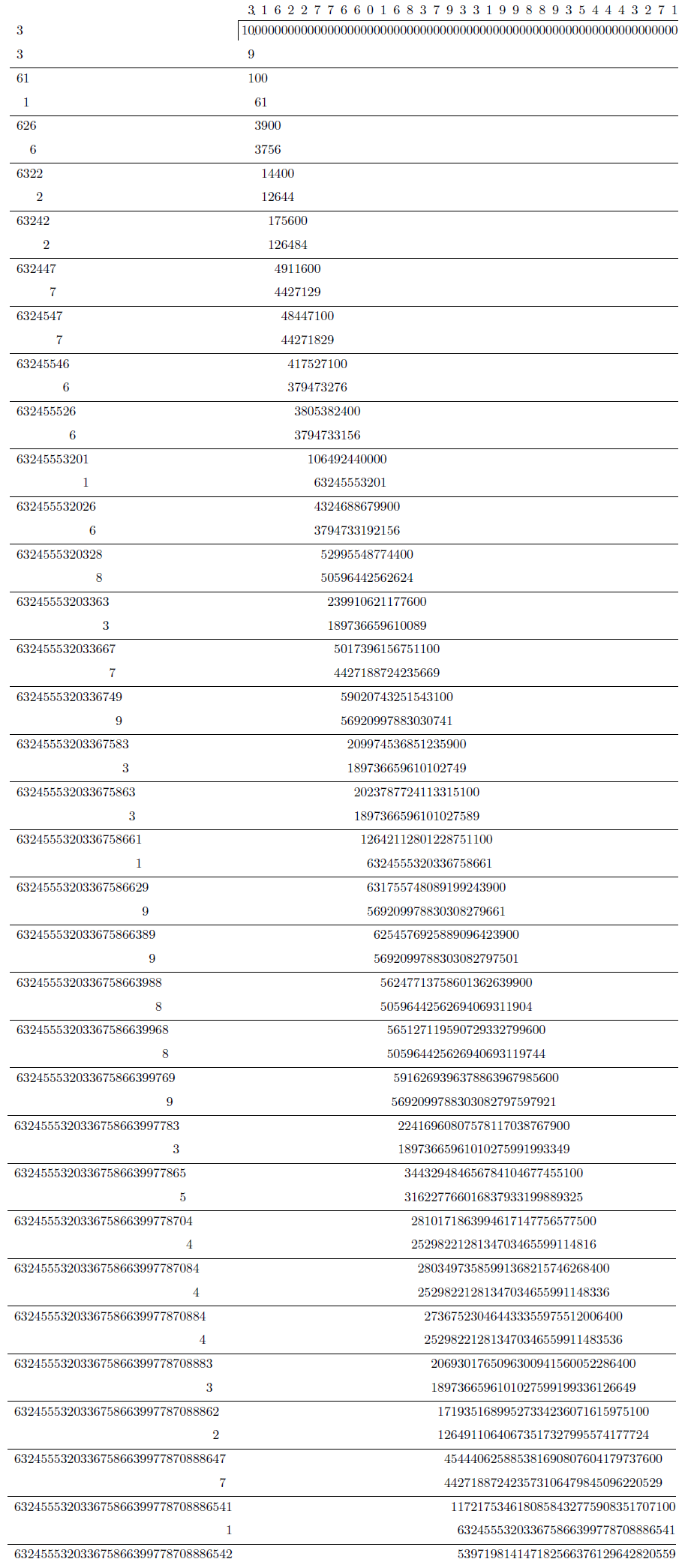
この1回分を54回繰り返し、10の254乗根を小数点以下32桁まで求める。さらに、同様にして2の254乗根も小数点以下32桁まで求める。後は、以下のような原理でlog₁₀2の値が求められる。

実際にブリッグスが行ったのはもう少し複雑な方法であった。対数表の作成には尋常でない労力が必要とされたわけである。
こうして出来上がった常用対数表を見せるために三度目の訪問を予定していた矢先の1617年4月、ブリッグスに一通の手紙が届いた。
偉大な先駆者ジョン・ネイピアが自分の城で旅立ったことの知らせであった(67歳)。数学史に名を残す二人が三度会うことは叶わなかったのである。
ブリッグスは、1617年に『1から1000までの対数』を公表した。彼の功績は、常用対数表の作成と共に、グレシャム・カレッジの力を総動員して普及させたことにもある。常用対数はもはや正弦に対する対数ではなくなり、一般的な数値計算においても利用できるようになった。
1624年にはブリッグスによって1から20000までと90000から100000までの14桁の対数表が発表され、さらに1628年にはオランダ人のアドリアン・ブラックによって20,000~90,000の10桁の対数表が発表され、対数概念の発見から約30年の長きを経てついに常用対数表は完成した。
また、ネイピアの死後2年後の1619年に息子のロバート・ネイピアによって出版された『素晴らしい対数表の作成法』では、小数の表現方法としてネイピアの対数表ではあえて避けていた小数点の使用を提案し、この発明も世界中に広がることになった。
計算尺の栄枯盛衰
1620年以降、対数の原理を用いる「計算尺」なる計算道具も登場し、有効数字3,4桁程度の計算ならば重い対数表を持ち歩く必要がなくなった。

Jakob.scholbach, CC BY-SA 3.0, via Wikimedia Commons
計算尺は様々な改良や目的別特化が繰り返され、電卓が一般的となる1980年頃まで理工系分野で重宝された。
日本の学校教育でも工業高校を中心に重要視され、つい40年前頃までは計算尺クラブが多くの学校に存在し、競技大会や検定試験も存在した。
2018年の大学入学共通テストの試行調査(2回目)では、計算尺に関する出題があった。


ネイピア対数の真の価値
ネイピア対数表で示されていたのは、log0.9999999(sinθ) の値であった。
累乗の間隔を狭めるためとはいえ、0.9999999の不自然さが否めない。ネイピアが底を0.9999999としたことは本当に合理的なものであったのだろうか。
常用対数が普及したこともあり、ネイピア対数は忘れ去られた。しかし、ネイピアの死後100年以上後、18世紀最大の数学者レオンハルト・オイラー(スイス;1707-1783)によって、ネイピア対数の真の価値が明らかにされた。

ーがついていることによって、0°<θ<90°のとき0<x’=sinθ<1より、y’>0となる。
そう、ネイピアは実質的に現在でいう自然対数(数Ⅲ)の概念に到達していたのであり、数学において円周率πと並ぶ最重要定数である自然対数の底eがネイピア数とも呼ばれるのも当然である。
現在、対数は単なる数値計算の簡略化のための道具に留まらない。オイラーによって指数関数の逆関数として対数関数が定義されて以降、対数理論として発展し、現代数学3本柱の1つである解析学の微分積分を根底から支えている。

