当ページには大学入学共通テスト(旧センター試験)過去問のネタバレ(問題と解答)がかなり含まれています。
過去問演習を行う前にネタバレを見てしまうと過去問演習の意味合いが半減してしまいます。
受験生は各自適切なタイミングで閲覧してください。
問題を解いた直後に閲覧するとリアリティが増すかも?
2020年に人類の前に突如現れた新型コロナウィルスによって部活動・大会・文化祭・修学旅行など普通の青春を奪われながらも受験勉強を頑張ってきたコロナ世代の高校生活の最後に待ち受けていたのは過去最大級の伝説であった。
センター数学では、制度が新しく変わって1年目は様子見で簡単になるが、2年目は難しくなる傾向にあった。
初めての共通テストとなった2021年のⅠAⅡBの合計平均点が過去10年間で最も高かったため、ほぼ全ての教師が「2022年は難しくなる」と予想していたし、また教師から言われて難しくなることを覚悟していた受験生も多かったであろう。自分も共通テストの1週間前に以下のツイートを残していた。2015年は難としているが、内訳はⅠA易ⅡB激難である。
共通テスト(旧センター試験)数学1A2B合計難度(平均点基準)
— 受験の月φ(.. ) (@examoonist) January 8, 2022
1997 易 新課程初
1998 難
2006 易 新課程初
2007 難
2015 難 新課程初
2016 難
2021 易 共通テスト初
2022 ?
このように多少の予感はあったわけだが、現実が想定を遙かに上回ってきた。
河合塾予想平均点速報の衝撃
数学の試験後のネットには、「難しすぎ」「隣の人問題破ってて草」「夢ならどれほどよかったでしょう」「難化ではなく進化」「女の子が泣き出した」などの意見が並んでいた。一言で言えば
阿鼻叫喚
阿鼻叫喚 人々が苦しみ泣き叫ぶような非常に悲惨でむごたらしいさま。八大地獄のうちの「阿鼻地獄」と「叫喚地獄」に由来する。
自分は「やはり今年は難しかったのか」と思う一方、「ほとんどは下位~中間層の受験生の意見だろう」と当初はそこまで気に留めることはなかった。
なぜなら、数ⅠAが伝説を残した2010年や2013年のセンター試験の時とは以下の2つの点が変わっており、共通テストの数ⅠAの平均点がそこまで大きく下がることはないと考えていたからである。
- 2021年の共通テストからⅠAの試験時間がセンター試験の時よりも10分増えて70分になった。
- 2015年以降、「場合の数と確率」「整数の性質」「図形の性質」が選択問題(2つ選択)になり、解けそうな分野の問題を選んで解答できる。
伝説誕生など全く予想していなかったが、平均点を日本最速でつぶやくのが毎年の目標(笑)なので、共通テスト2日目が終わって数時間後に発表される河合塾と駿台の予想平均点速報(一部の塾生の結果と予備校講師の勘によるのでかなり適当)をF5アタックをかましながら待った。
先に速報を発表したのは河合塾。それを見て過去一番の衝撃が走る。
数学ⅠA 38点 数学ⅡB 42点
「いうおうjたう;pええええ?????????????」と日本語で表現できないような第一声を発してしまった。
10年以上共通テスト(旧センター試験)の平均点を追い続け、以下のページまで作成している自分にはダブルの衝撃である。
1つ目の衝撃は何と言ってもⅠAの圧倒的な低さである。
実際に受験生を指導した経験があれば、受験生目線で難易度変化を感じ取ることができる。「今年の数学は受験生には難しいかな」と感じられるほどの難易度変化があるときには、大体100点満点で5点ほど例年よりも平均点が下がっている。難易度変化の平均点への影響は意外に小さく、体感でわかるほど難しくなったとしても平均点の変化は通常5点下がる程度に過ぎないわけである。
平均点が例年より10点も下がろうものなら、もはや入試の伝説として語り継がれるレベルの難度であったといえる。
1997年に現在のⅠAⅡBの形式になって以来、センター数学の例年平均は概ねⅠA60点、ⅡB50点であった。この例年平均に対し、10点近く平均点が低くなった2010年ⅠA(48.96)、2013年ⅠA(51.20)、2015年ⅡB(39.31)は伝説となった。



河合塾のⅠAの予想は、過去最悪の2010年の伝説時の48.96よりもさらに10点以上低く、こうなるともう何が起こったのか皆目見当がつかない。
- 2013年ⅠA (51.20) 大問3で壊滅的被害
- 2010年ⅠA (48.96) 大問3と大問4で壊滅的被害
で・・・伝説の2013年を超えた2010年の難度を・・・さ・・・さらに超えた・・・!?
2つ目の衝撃は、ⅡBの平均点も過去3番目の低さだったことである。過去数学の平均点が低くなることは何度かあったが、ⅠAとⅡBはある意味バランスが取れていて、一方が難しくなると他方が簡単になってⅠAⅡBの合計平均点は常に100点以上あった。
しかし、河合塾の合計80点という予想は過去最低よりも20点以上低く、前年比では-37点である。900点総合で前年比-37は過去何度かあったが、数学だけで-37点というのはもはや現実とは思えない。
「去年様子見をした共通テストが本気を出したのかな?試行調査のときは平均50点を目指すという話があったくらいだし。。。これボーダーラインどうなるんだろう?う~ん、全く読めない・・・」
などと考えているうちに発表された駿台の予想は ⅠA 43点 ⅡB 50点
河合塾とは合計13点ものズレ。河合塾の低すぎる予想をにわかには信じがたく、この時点では「なんだかんだで駿台の予想に落ち着くのではないのか?河合塾の予想適当すぎwww」などと思っていた。
変異した共通テスト
2日後、河合塾と駿台の40万人(全受験生の約8割)の正確な集計結果(予想平均点確定版)が発表される。これらは毎年公式の最終発表とのズレが非常に少なく(各科目1点未満)、2022年共通テストの平均点がほぼ確定したことになる。
ⅠA38点、ⅡB43点でまさかの河合塾がほぼピタリ賞。今年の数学ⅠAの伝説入りが確定。
一体何が起こったというのか。
問題を入手後ざっと一見するも、去年より平均点が20点も下がるほどの難しさは感じられない。
伝説の2010、2013、2015年の平均点が低くなったのには共通の理由があった。大問の序盤に難しめの穴埋めがあり、そこを乗り越えられなかった多くの受験生が他科目ではあり得ない大問丸ごと失点の憂き目に遭ってしまったのである。
しかし、今回はどうも違うようだ。調査していると、既に問題を解いた教師達が「問題を見ただけでは判断できない。時間を計って実際に解いてみるとわかる。」と口を揃える。
で、自分も解いてみた。
「つ・・・ついに本性を現したか・・・これが真の胸痛テスト・・・」
2021年の共通テスト数学には、「言うてもセンター数学の延長線上かなあ」という印象をもっていた。しかし、2022年の共通テスト数学にはもはやセンター数学の面影はほとんど感じられない。完全に変異した別物である。
試験前は「多少難しくなっても所詮は共通テスト。難化の影響を受けるのは中間層と文系だけで難関国立2次記述試験レベルの演習を十分に積んできている自分達は大丈夫。」などと余裕をかましていた理系上位層受験生も多くいただろうが・・・
「共通テストを舐めるなよ。お前達は何にもわかっちゃいねぇよ・・・」
共通テストの底すらない悪意(進化)を・・・・・・!!
運命の70分間
2022年受験生の運命の70分間を1問ずつ振り返っていく。
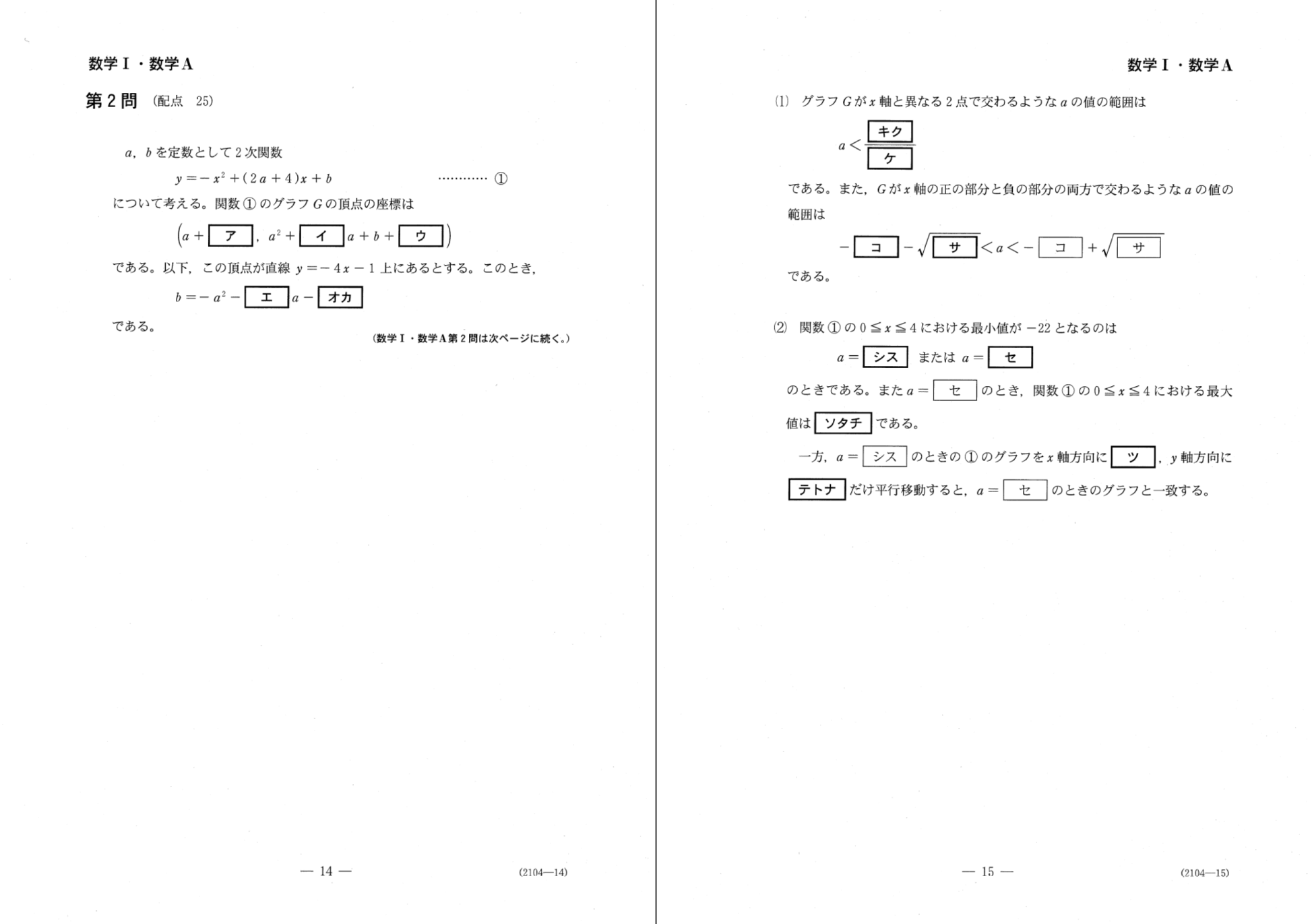
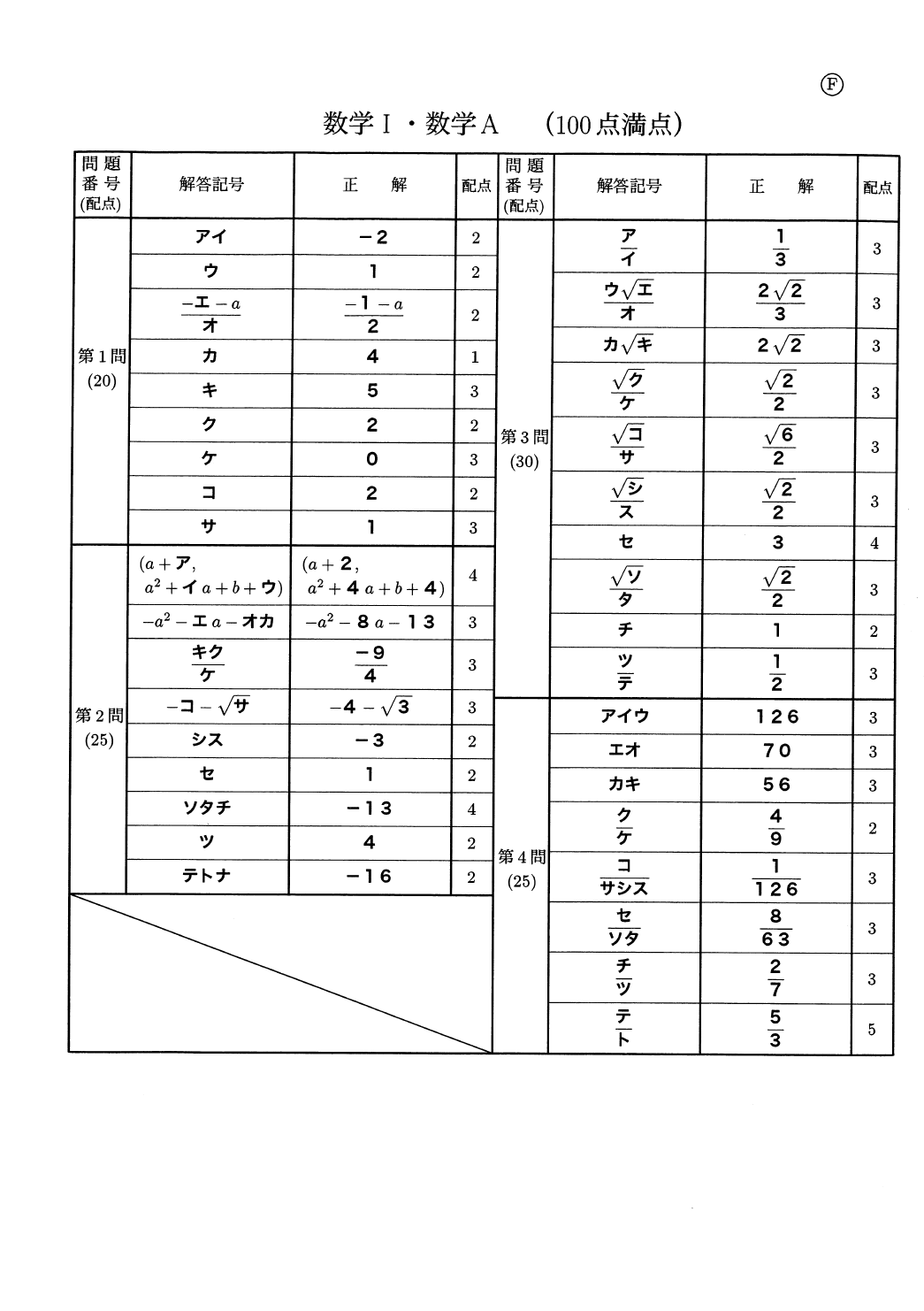
第1問 [1]


センター数学を思い起こさせる今回唯一といっていい良心であり、うまく誘導に乗って行けば5分程度で満点の10点を獲得できる。
しかし、文字が多く紛らわしかったせいか、(2)の出来はそこまでよくはない。
人生をかけた一発勝負の大一番、受験生本人が意識していなくてもその心理は極限の緊張状態にある。この点においては上位層も下位層も関係ない。
一旦沼にはまるとそう簡単に抜け出せないのがマーク数学の恐ろしいところである。
後で解説を見て「あ~もう、こんな単純なことだったのか・・・」と悔やんだ受験生も多かっただろう。
今年のⅠAは、ここで失点してしまうと50点を超えることが一気に難しくなる。「難易度が低い」「時間がかからない」「高配点」の3拍子そろった問題が他にほとんどないからである。仮に失点したとしてもあまり時間を使っていなかったのであればまだ救いはあるが、粘った挙げ句に失点してしまった場合、この時点で2022年の数ⅠA壊滅がほぼ確定する。
運良くちゃちゃっと解けた受験生は「全然難しくなってないな・・・意外といけるかも♪」などと楽観視していたかもしれないが、次々と登場する悪意に時間と気力がものすごい勢いで削られていくことになる。
第1問 [2]
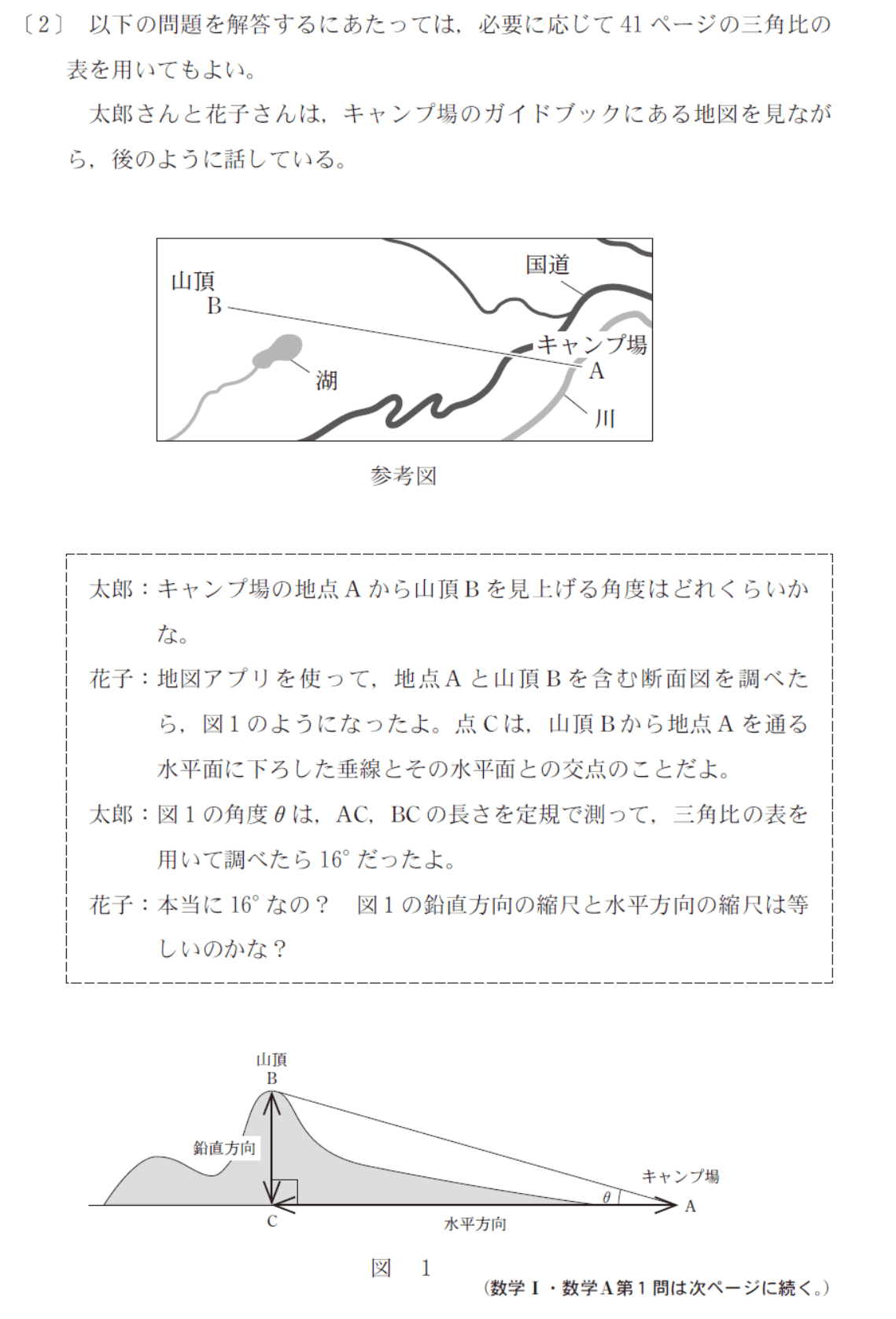

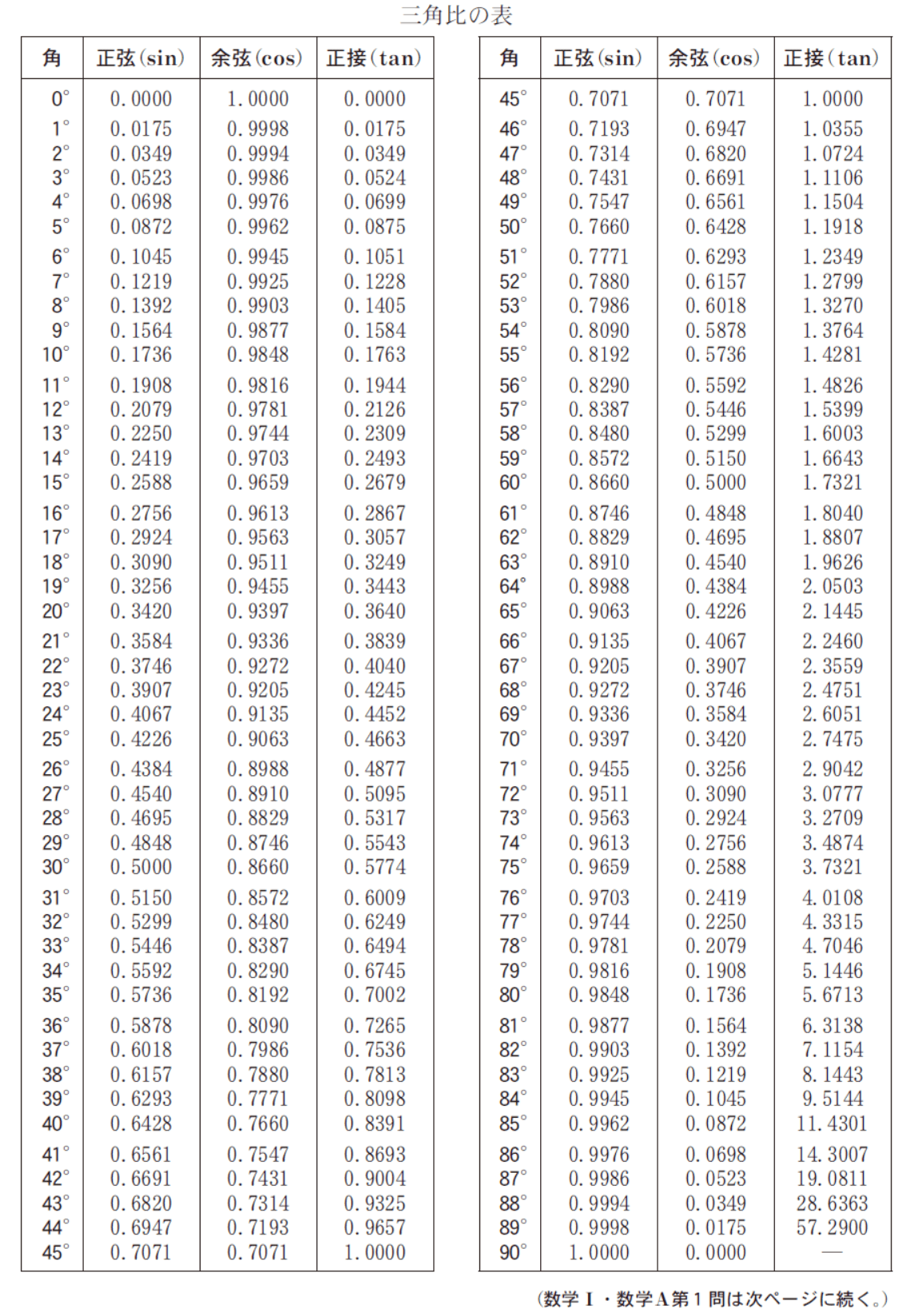
早くも共通テスト数学を象徴する太郎・花子が登場し、解答に全く必要のない無駄話を開始する。
「ざっと読み流して要点をつかむことが大事」「読解力の低下だ」などと適当なことを抜かす部外者も多いが、科目の違いおよびマーク数学と記述数学の違いを全く理解していない。
マーク数学では、まずは問題文を丁寧に慎重に読むことが鉄則である。国語や英語では語句1つ読み間違えたところで大した影響はないが、読み違え1つで雪崩式に大量失点してしまう可能性があるのが数学の恐ろしいところである。また、他科目のように難問でも勘で当たるといったことがないため、解けるはずの問題での失点は絶対に許されない。高得点狙いの人ほど、簡単な問題では慎重に慎重に万に1つのミスもしないように注意しながら確実に正解を積み重ねていかなければならない。加えて、記述試験ならば大筋が正しければ多少のミスは大目に見て部分点をもらえる可能性がかなりあるが、答えだけのマーク数学ではミスると当然0点である。
「読み流す」などというのは単なるギャンブルプレイであり、受験生にはリスクが大きすぎる。不幸にも、このことは今回の試験で早くも証明される。時間に追われてギャンブルプレイをした受験生がどれほど悲惨な目に遭ったのかが後半で明らかになる。
ただし、本問ではむしろ慎重さが裏目に出る。
問題自体は単純で、結局はtan16°の値を三角比表から読み取り4で割ればよいだけなのだが、0.2867÷4=0.071675となり、マーク欄にうまくはまらないのである。
「あれ?どこか間違ってる?もう一度やり直そう。」「もしかして四捨五入かな?でも問題に指定ないし。。。まさか切り捨てじゃないよね?」などと確信が持てないまま無駄に時間を消費してしまう。
本問における正解プレイは何だったのか、それは「裏表紙の注意事項を読んでおく」である。
表紙に「必ず読みなさい」とまで書いてあるから読んでなかった受験生が悪いよね(;>_<;)
表紙

裏表紙

四捨五入と切り捨てで答えが違ってくるというのも非道い嫌がらせである。注意事項を読んでいなかったとしても大抵の受験生は四捨五入したと思うが、中には切り捨ててしまった受験生もいたようだ。
2021年本試や2022年追試では問題に指示があったから、なぜ2022年本試では問題に指示がなかったのかは不明である。「ルールすら確認しない受験生にプレーする資格はない」的なことを訴えたかったのだろうか。
最悪なのは、このトラップが試験の序盤にあったことである。試験の後半で既に時間に追われた状態であったならば、「余計なことを考えている時間はない。四捨五入しよう。」などとすぐに割り切ることができたかもしれないが、まだ時間がある段階なので深刻な戦略ミスであることに気付かずに考えすぎてしまうのである。単純な問題ですぐ目の前に正答があるからこそ即断することが心理的に困難になる。試験の後半になって、「ああああああ、前半くだらないことで悩んで時間を使っている場合じゃなかったんだ。。。さっさと四捨五入して先に進んでいれば・・・」と気付いても後の祭りである。
試験慣れした受験生ほど「四捨五入が必要になる場合は問題に書いてあるはず」などという先入観を持っており、勝手に「これからもそうであるはずだ」という自分に都合のよい思い込みをしてしまいがちである。かなり昔だが、以前にも突然の傾向変化に多くの受験生が翻弄されたことがあった。
1985年、センター試験の前身に当たる大学共通第1次学力試験のときのことである。いわゆる共通1次数学では、マーク欄から答えの桁数を絞らせないためにマーク欄が余る場合は米印に似たアスタリスク「*」をマークする決まりであった(センター試験からはこの制度はなくなった)。例えば、マーク欄が[アイウ]だったからといって、答えが[120]や[-12]とは限らず、12の可能性がある。この場合、[12*]と埋める決まりであった。ただ、1979年に共通1次が始まって以降、1985年になるまで「*」が必要になったことはなく、多くの教師や受験生は「*が必要ならばミスを疑うべき」と思い込んでいた。しかし、1985年になって突如「*」が頻出し、多くの受験生は激しい動揺に見舞われた。
これが極一部で語り継がれている「昭和の米騒動」である。
本問のトラップはこれだけではない。
時間制限が厳しい試験においては、「点数の対時間効率」が戦略上重要である。
試験時間は70分であるから、仮に目標点数が70点であったとしても、単純計算で1分あたり1点取らなければならない。時間をかけすぎると、せっかく問題が解けたとしても総合的に見て損をしていることになってしまう。点数効率を考慮した時間配分が要求される。
しかし、厄介なことに、中問・小問の細かい点数配分は解答を見るまでわからない。受験生は闇の中を手探りで進んで行くしかないのだ。
終わってみれば、今年の第1問の点数配分とページ数は次であった。
[1] 10点 (2ページ) [2] 6点 (3ページ) [3] 14点 (1ページ)
つまり、最も文章量や文字数が多い[2]は、最も短時間で終えなければならない問題だった。本問に時間をかけた受験生は、気付かぬうちにすでに恐ろしい罠にはまっていたわけである。
それでも時間をかけて正解できたのならばまだいいが、自分が簡単だと思ったこの問題、受験生の出来が非常に悪い。おそらく正答率は2割ないのではないか。速攻で捨てた受験生も多い上、70点以上取ることができた上位層でも普通にこの問題を落としていたりする。受験生の多くがこの手の問題を苦手とすることはわかっていたが、ここまで悪いとは思っていなかった。「思考力を問う」という共通テストの目的および、以下の元ネタを回顧するという意味でも、個人的にはいい出題だったと思う。
本問は、2019年に問題になった自衛隊の陸上配備型イージス・システムの設置に関するずさんな調査を元にしていると思われる(大学入試センターはやんわり否定しているが具体的な数値までほぼ一致)。鉛直方向と水平方向の縮尺が異なったままでレーダーの電波が遮られる山の仰角を計算し、約4度が正しいところを約15度と記載してしまうという非常にお粗末なものであった。
第1問 [3]
[2]で共通テスト形式になったかと思いきや、なぜか[3]では再びセンター数学に回帰する。

基礎レベルの(1)で5点稼げるが、9点分の(2)が普通に難しい。
「(2)はちょっと時間がかかりそうだな。後回しにしよう。」と判断した受験生も多かったはずである。それ自体は戦略的に間違いではないが、無事に生還してこの問題と再会できた受験生がどれだけいただろうか。十中八九、永遠の別れになる。
なお、大学入試センターの発表によると、[ソタ]の正答率は約75%、[チツテ]の正答率は約55%であったという。
これは、「大学受験生のうち4人に1人は正弦定理を覚えていないか、あるいは覚えていてもまともに使いこなせない、さらに、正弦定理を使いこなせる受験生であってもそのうち4人に1人はそもそも正弦とは何かがわかっていない」ことを意味している。
第2問 [1] (1) (2)
太郎・花子が消えてくれて喜んだのも束の間、太郎・花子再登場。

まず(1)で確実に4点稼がなければならないが、急いでいると間違える。
(2)はいわゆる共通解問題であり、パターン認識できていれば何のことはないが、平均レベルの受験生の多くはパターン認識できていないので厳しくなる。
誘導が親切に見せかけて実はかなり不親切なので、簡単に求まりそうで求まらない。一見するとqの2次方程式でも作成できて[ウ]と[エ]が両方一気に求まりそうにも思えるが、そんなに単純ではない。しかも、誘導に乗って求まるのは[ウ]だけで、[エ]は自分で全く別の観点を考慮して求める必要がある。案の定(2)は出来が悪い。
まともにやると(1)と(2)で何度も何度も2次方程式を解く羽目になるので、思った以上に時間と気力を消費する。
大小関係が指定されているので両方求めないと正確に埋められない上、この結果を利用する(4)に手がつけられない。
第2問 [1] (3)

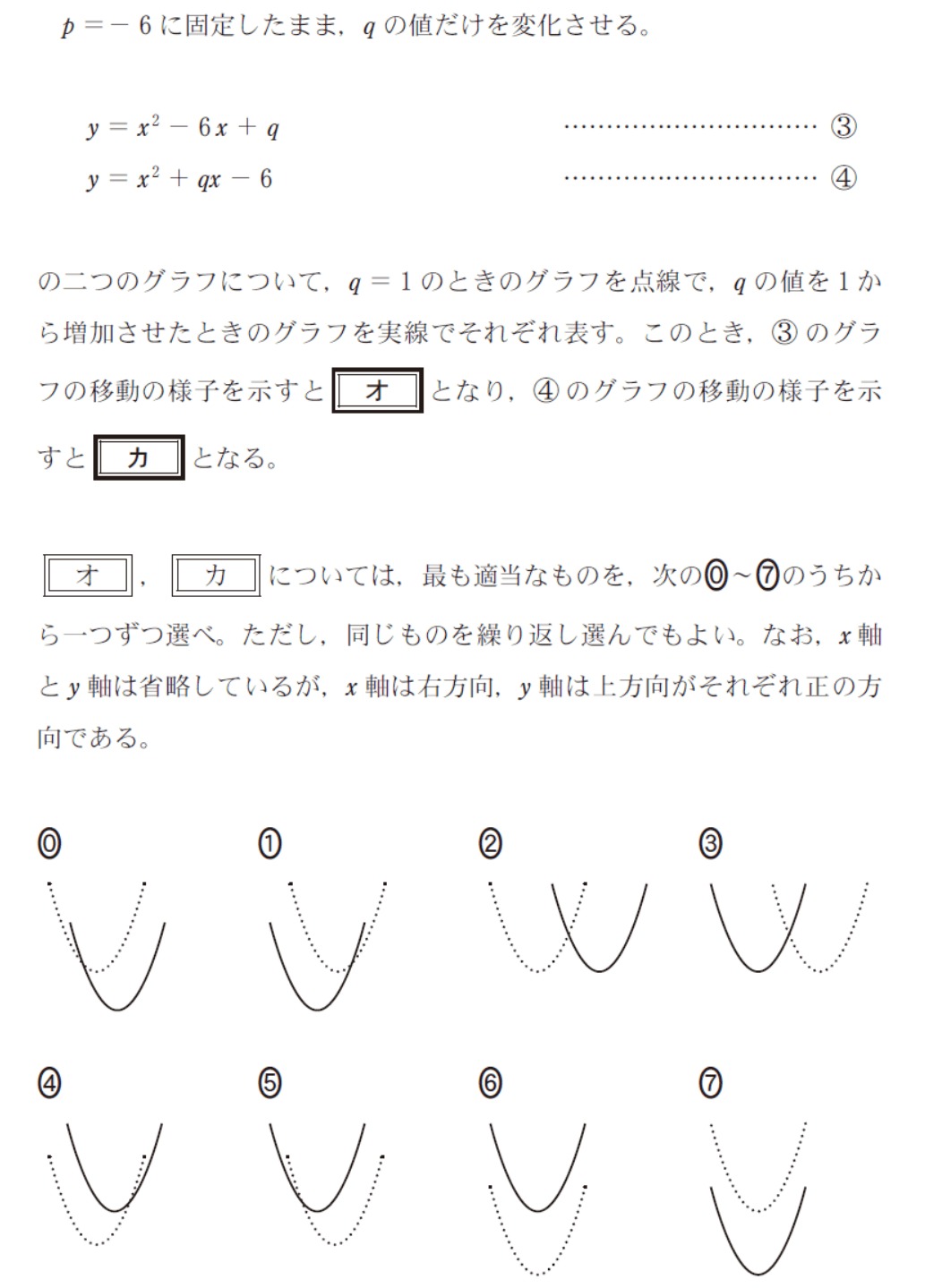
イラストが気になって「花子さん楽しそう」「ちゃんとマスクしてる」「高校生に見えない」などとくだらないことを考えていると貴重な試験時間が数秒削られる(笑)。
簡単で短時間で解けるので正解者も多いだろうが、[オ]は1点、[カ]は2点なので思った以上に点が伸びない。
第2問 [1] (4)

恐ろしい問題である。
センター試験はもちろん、2次記述試験においてもこれほど恐ろしい問題は見たことがない。
(2)ができている必要がある上に相当な難問なのだが、この問題の真の恐ろしさは単に難問だからということではない。
通常の難問ならば、「これは後回しにしよう」などとすぐに割り切って先に進むことができる。しかし、必要十分条件の問題では4択であり、さらに必要か十分のどちらかだけでも判断できれば2択になる。よって、受験生は簡単に捨てたり後回したりすることができず、「少しでも正解に近づきたい」と粘ったはずだ。
それでも難しいものは難しい。問題の意味を正しく解釈し、さらに正しい思考の元で確信を持って答えられた受験生がどれだけいただろうか。最終的には「う~ん、今一つ自信が持てないけどこれかなあ。頼む、正解であってくれ。」などと祈りつつ埋める羽目になる。
受験生のその微かな希望に対し、共通テストはあまりにも無慈悲だった。
自分もこの問題を解いた後、「いや~これは難しいなあ。[キ]と[ク]それぞれ3点くらいかな。」などと思いつつ解答を確認して戦慄した。

「うっっっそ、これ両方正解しないと点もらえないじゃん。。。しかもたった3点。。。」
いきなり「必要でも十分でもない」という選択肢は心理的に選びづらく、勘で当たる可能性もかなり低い。
最悪運でも何点かは取れる可能性があるように見せかけて受験生の意識を束縛して貴重な試験時間を浪費させ、結局1点も与えない、挙げ句の果てには正解できたとしても5分もかけていると点数効率的に大損するという凄まじいトラップである。結果論でいえば、速攻で捨ててもよい問題であった。実際に試験を受けている受験生が非常に取りづらい戦略が正解だったわけである。
第2問 [2]
早くもかなり追い詰められつつある受験生を次に待ち受けるのは、2015年の初登場時から「統計の重要さ自体に疑う余地はないが、果たして数学の試験に必要なのか?」と悪名高いデータの分析である。
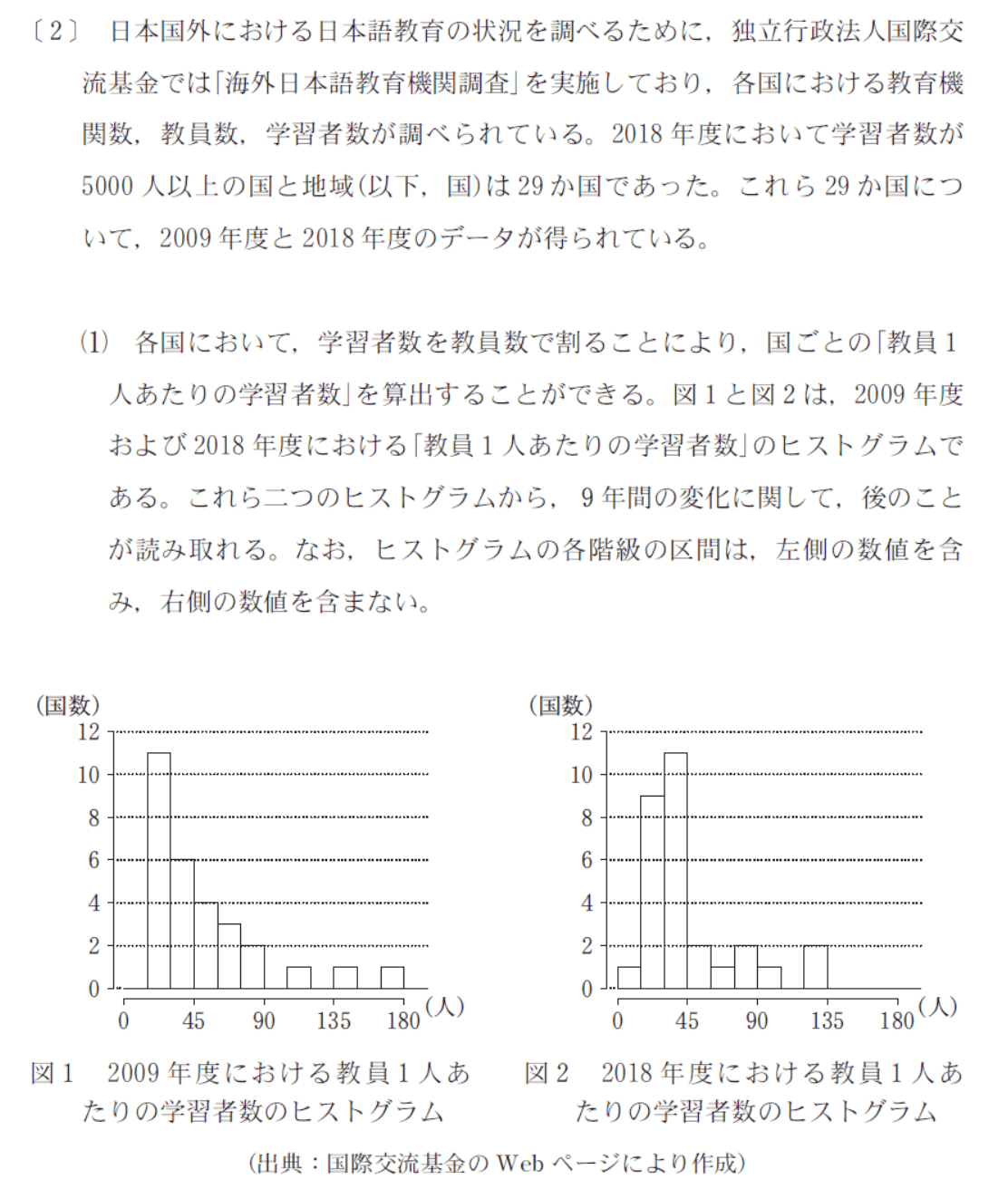

データの分析は、数学が苦手な学生には得点源になるので好まれるが、数学が得意な学生にとっては無駄に時間を消費させられる嫌がらせでしかない。
いきなりの長文、「どうせ読む必要ないのだろう」と思いつつ一応読むも、案の定ほぼ必要ない。
さっさと終わらせてしまいたいところだが、例によって慎重さを欠いていると一瞬で0点にされる配点である。しかも、[ス]がやや難しい。
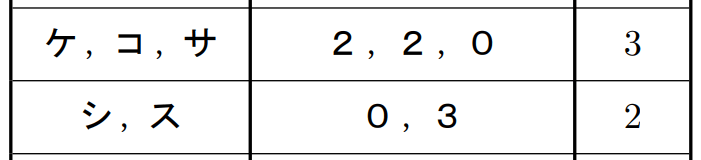
第2問 [2] (2)


箱ひげ図とヒストグラムから散布図の選択。
他と明らかな違いのある①だけはすぐに消去できるものの、他の3つの違いが少なすぎて簡単に判断できない。結局ちっこい白丸を1個ずつ数えるしかなく、時間がない中での視力検査を強いられて泣きたくなる。
これが2022年数ⅠA唯一の4点の高配点なので、安易なミスは命取り。
第2問 [2] (3)
試験も中盤にさしかかり、この頃から残り時間がかなり気になってくる。
焦りを隠せなくなってきた受験生を、時間・集中力・気力がすべて奪われる最悪の問題が待ち受ける。

「どれどれ・・・2018年を基準とした2009年の値がS,Tか・・・それから・・・例も示してあるのか・・・なるほど・・・御丁寧に共分散の定義まで書いてあるな・・・で、結局何をやれば・・・」
「相関係数を公式に当てはめて計算するだけじゃねーか!!!」
時間のない中でせっかく理解した長文は解答に全く必要なく、相関係数を求める公式(SとTの共分散)÷(SとTの標準偏差の積)を覚えているかだけが問われている。
数値がうざいことこの上なく、何をさせたいのかが全くもって意味不明で問題用紙を破り捨てたくなってくる。ただ、誰でも解ける問題を捨てるわけにもいかないので、受験生は否が応でも計算地獄に落ちていく以外にない。
自分は、以下のような手順で絶対にミスしないように慎重に計算して2分ほど要した。
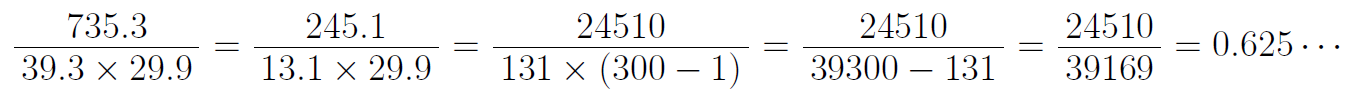
心の声 7+5=12(3の倍数条件)だから735.3と39.3が約分できて・・・小数は鬱陶しいから整数にして・・・299=300-1として・・・131=130+1とすると余計面倒そうだな・・・よし、後はゴリ押そう。しんど。
脳内にそろばんでもあれば話は別だが、並の受験生ならば丁寧にやっていると3,4分はかかる。四捨五入を考慮すると小数第3位までの正確さが必要であるから、わずかなミスも許されず高い集中力が要求される。最後の最後、割り算の筆算を油断して0.624・・・などとしてしまうとすべての計算が水の泡になる。時間を浪費する割に3点なので点数効率が悪い。
ただし、時間のかからない(4)と連動しており、(3)(4)を合わせると6点で素早く計算できるならば割と点数効率はよいという複雑すぎる問題構造で、もう戦略的に何が正しいのかが全然わからない。
そして、厳しい時間制限と極度のプレッシャーがある中で「正確に」四則演算するというのは決して簡単なことではない。
時間をかけて必死に計算したにもかかわらず、自己採点でミスに気付いて卒倒しかけた受験生も多かったであろう。しかも、正解からあまりにも大きくずれていると、この結果を利用する(4)でも失点してしまい、小学生レベルの計算のせいで6点失うという地獄のような結果になる。
第2問 [2] (4)
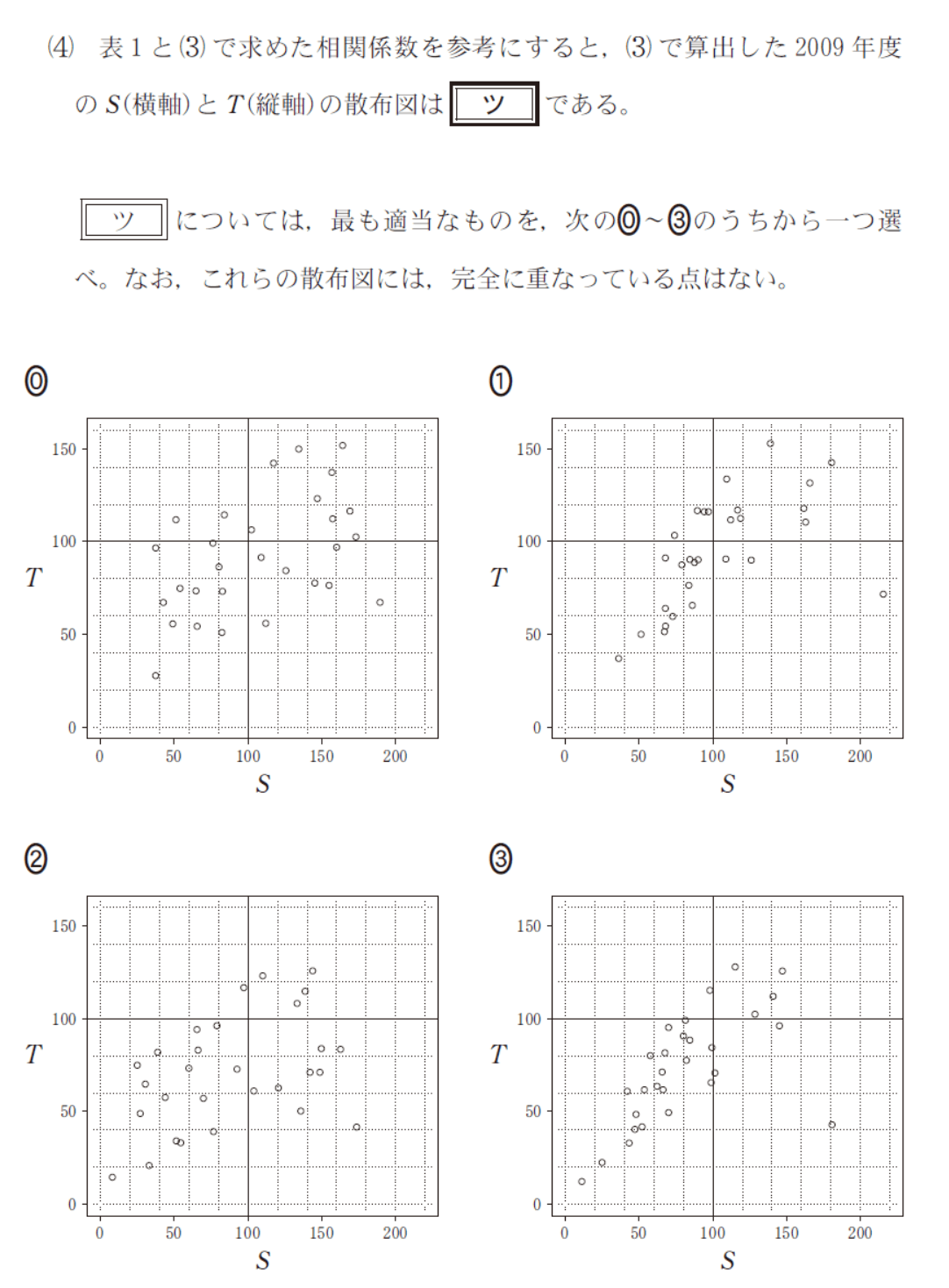
データの分析のラストは、(3)で求めた相関係数(と平均点)を元に散布図を選択する問題である。
センター数学でも同様の問題があったことから、以前から散布図と相関係数のおおよその対応を見た目で判断できるべきであることを主張してきた(これって数学なのかな?)。
しかし、⓪と②はほぼ0、①と③は0.8くらいに見えて、(3)で求まった約0.6にふさわしい選択肢が見当たらない。「あれ?」と思いつつ、消去法で何とか自分は正解できた。
どうやら、①と③は右下の外れ値を除くと約0.8だが、外れ値を含めると約0.6となるということらしい。
それは知らんわ
問題作成者が、外れ値がこれだけ相関係数に影響を与えることを知らしめたかったのであれば、この出題は成功したといえる。
第2問までで点数配分的に6割終了、実際に問題を解いてみるとわかるが、難易度・文章量・計算量・思考量の壁に阻まれて全然先に進めないので肉体的・精神的疲労感が尋常ではない。数学の問題を解いているだけのはずなのに、全力で100m走し終えた後かのように呼吸が苦しい。
配点を考慮すると、単純計算では第1問21分、第2問21分、第3問14分、第4問14分が適正時間である。
残り時間とここまでの出来から、受験生は薄々勘づき始める。
「過去最悪の結果になるかもしれない。」
諦めたらそこで試合終了。問われたのは、悲惨な未来を予期しつつも最後の1秒まで粘り切る強靱なメンタル。
第3問 (1)
第3問の場合の数と確率では、完全なる差別化が行われた。
「知る人」と「知らない人」

プレゼント交換の問題は、いわゆる完全順列(モンモール問題)と呼ばれる超有名パターン問題である。
「知る人」ならば、この第3問を3分程度で完答することができる。「知る人」とは、以下のページにあるような完全順列の解法・漸化式・一般化公式の知識を十分に理解・暗記できていた受験生のことである。
「最も思考力を問えそうな場合の数と確率でパターン問題出すんかい」ともちょっと思ったが、難易度が高いパターンであるため、難関大学受験生でも十分に理解・暗記できている学生はかなり少ない。かなり高いレベルまで学習していたごくごく一部の受験生への文字通りのプレゼント問題であった。
結局、ほとんどの受験生は「知らない人」である。初見か、あるいは「そういえばそんなのがあった気がする」という程度のほぼ初見に近い状態であり、この場合はすべて書き出して数えることになる。
まあ、2人や3人なので(1)はすぐに終わる。2人での交換会さびし~(つД`)
ただし、油断は禁物。「全員が自分以外」というのは意外と複雑な条件なので、焦っていると普通に間違える。大抵のミスを吸収するマーク欄なので、ミスに気付けない。
第3問 (2) (3) (4)

(2)は正攻法に気付けたならばすぐに求まるが、初見で厳しい時間制限の中で気付くのは容易ではない。穴の形から多くとも9通りしかないことがわかるが、すべて書き出して考えていると結構な時間がかかる。
そして、序盤の伏線を回収するときが来た。
マーク数学では、「時間がかかっても問題は丁寧に読むべき」なのであった。
時間に追われて愚かにもそれを怠ってしまった受験生に恐ろしい天罰が下る。
「終了しない」場合の数を求めた直後の「終了する」確率トラップ発動
面白いように引っ掛かる正に入れ食い状態。これがまたうまいこと穴にはまりやがるからミスに気付くこともできず、同じ考え方を用いてより多くの時間をかけて求めたはずの5人の(3)(4)にまでミスが連鎖する地獄絵図と化す。
先程のリンク先のページでは、「5人の場合まで暗記しておくといいかも?」とまで記載していた。暗記していれば、トラップのリスクもなく文字通りの瞬殺であった(ふふん♪)。なお、共通テストで役立つことは想定外(・∀・;)
第4問 (1) (2)
第4問の整数分野は、直感的な理解が難しいために下位層は苦手としているが、型にはまった問題が出て学習が得点に反映されやすいため、数学が得意な学生に好まれる。第3問の場合の数と確率および第4問の整数を選択することを最初からある程度決めている上位層も多いことだろう。
自分は3年ほど前から毎年事前につぶやいていた。
共通テスト(旧センター試験)数IA整数の出題内容㊙️
— 受験の月φ(.. ) (@examoonist) January 5, 2022
2015本 ax+by=1
2015追 ax+by=1
2016本 ax+by=1
2016追 ax+by=1
2017追 ax+by=1
2018本 ax+by=1
2018追 ax+by=1
2019本 ax+by=1
2019追 ax+by=1
2020本 ax+by=1
2020追 ax+by=1
2021(1) ax+by=1
2022 ❓

今年の出題も1次不定方程式ax+by=1で、見事予想的中(?)。
最初のx,yは5⁴÷2⁴を計算するだけだが、すでに集中力が喪失した上に時間に追われていると通常では考えられないようなミスをしてしまうのが一発勝負本番の恐ろしいところである。
「時間がない!急げ急げえええ!2⁴=8だから 625÷8=78・・・1 になって、つまりは 625×1-8×78=1 だから x=1,y=78 だ!」
といったように、とんでもないやらかしを犯したとしても穴の形でミスに気付けず、次のx,yにまでミスが連鎖する。
次のx,yは最低限のax+by=1の解の構造を理解していれば瞬殺なのだが(ただしーに注意が必要)、理解している学生は多くない。普段通りに 5⁴(x-1)-2⁴(y-39)=0 などとやっていると、1,2分余計に時間がかかる。
(2) [コ]は(1)の誘導でもあった 625=2⁴m+1 の両辺を2乗するだけであることに気付ければ一瞬だが、時間に追われていると意識が(2)だけに集中してしまうので思いの外気付きにくい。
[ケ]と[コ]は両方正解して2点であり、[ケ]を埋めただけで1点もらえるほど真・共通テストは甘くはない。[コ]をm=39を代入してゴリ押しで求めた受験生もいた。
第4問 (3)

多くの受験生は時間的にここまで辿り着けないか、辿り着けたとしても誘導の意味不明さと答えの桁数で心が折れる。(3)(4)だけで20点中の11点を占めているから、第4問の整数が5割を切る。
高得点を目標とする上位層は果敢に立ち向っていく。誘導に一旦乗ってしまえばxは10秒で求まるが、そもそも乗ること自体が難しい。
誘導の解読に四苦八苦していると、「これ誘導無視してゴリ押しで求めた方がいいのでは?」という誘惑が頭をよぎり出す。係数がやたらとでかいだけで所詮は1次不定方程式である。modを利用する方法やネットに転がっている裏技的な方法を習得済みであったならば、ユークリッドの互除法を用いる一般的な方法よりも楽に求められる。
いずれにしてもゴリ押しは計算ミスのリスクが大きくなるのである種の賭けであり、数学力に加えて覚悟・勇気・決断力・精神力そして運が必要である。
思い返せば、第4問に取りかかる直前に問題をざっと眺めた時点で5桁のyに気付き、かなり嫌な予感はしていた。
それでも、多くの受験生はあまり慣れていない第5問「図形の性質」を本番でいきなり選択する勇気もなく、そもそも問題選択の時間的な余裕すら与えてもらえなかったので第4問を選択せざるを得なかった。
また、少しは期待をしていた。
「誘導にうまく乗れたら実は簡単に求まるのかも・・・そうに違いない。見た目だけでビビっては駄目だ。」
しかし、真・共通テストに見事にその期待を裏切られ、嫌な予感が現実のものになる。
何とかx=125が求まっても、結局これを②に代入してyの値(5桁)を求めるしかなく、ここまできてのこの数値計算は悪夢としか言いようがない。(2)を利用する(正攻法?)と多少楽になるが、まずもって気付かない。
自分が初見のときに真っ先に思い浮かんだのは、○5²の速算を利用する以下の手順であった。625×625は、62×63を計算すれば済むことを知っていたのだ。
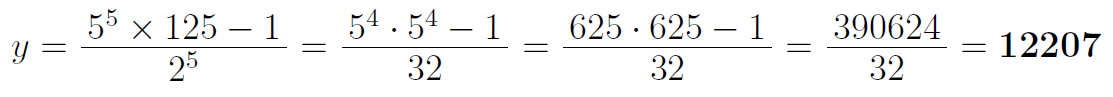
そのすぐ後で下の因数分解する方法にも気付いたが、もうすでに計算を始めていたので最初に思いついた方法を優先した。後で検証してみると、自分の場合上の方法は約30秒、下の方法は約1分を要した。上の方法が本質的に有利だったわけではなく、たまたまyの各桁の数字が小さく÷32の計算が容易だったおかげである。
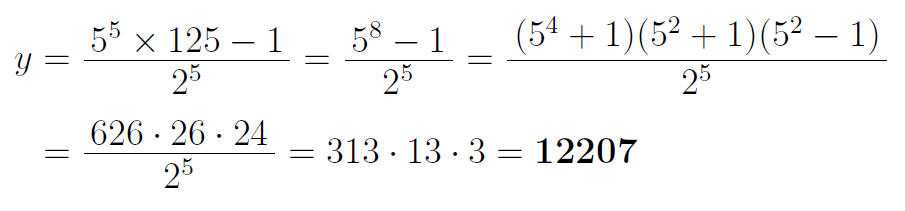
例えばだが、何かを間違えてx=123と求まってしまったとする。この場合、計算の工夫の余地もなく必死に計算してyを求めようとした結果・・・
「ああああ、32で割り切れずyが整数にならないよおおお。x=123が違うのかあああ。また一から考え直さないとおおおお。」
てな感じで一旦沼にはまると、思考して計算して思考して計算して思考して計算してとなってもうパニックを超えた狂乱状態に陥る。
さらには、xの導出の際に0を忘れたために1つずれたx=157が求まってしまった受験生もかなりいたようで、この場合は地獄の計算 y=(5⁵×157ー1)÷32 をさせられた挙げ句にyが綺麗に整数になるのでミスに気付けない。
ミスに気付いても地獄、気付かなくても地獄。
第3問の場合の数と確率もそうだが、手も足も出ないわけではなく、ゴリ押しする方法が容易に思い浮かぶ点がある意味厄介で、優先順位の判断に迷いが生じて不安が増大する。正攻法がわかるまで粘るか、ゴリ押ししてしまうか、速攻で捨てるか、運にも左右されるので何が正しかったのかは結果論でしか語れない。
あと自分は以前から主張しているのだが、中高生は最低限の速算術を習得しておきたい。
個人的オススメ4選 実戦で役立ち、習得が容易で、応用も可能。

実戦でいきなり使うのは難しいので、普段からこのように計算する癖をつけておくことが重要である。
相関係数の計算で「なんで29.9なの・・・時間がないのにもう~~~」と泣きべそをかきながら計算せずに済んだし、計算量が減るとその分ミスのリスクも減る。
他にもいろいろあります。
第4問 (4)
瀕死の状態で命からがら(4)までたどり着いた受験生を問題作成者の恐ろしい悪意が待ち受ける。
絶対に満点を取らせない

「残り3分。まだいける。え~と・・・要するに本質的には(3)と同じだな。(3)と同様に考えると・・・xの1つは11³・・・計算すると・・・1331・・・これを32で割ると・・・41あまり19だから最小のxは19!残り1分、後はyだけ!」
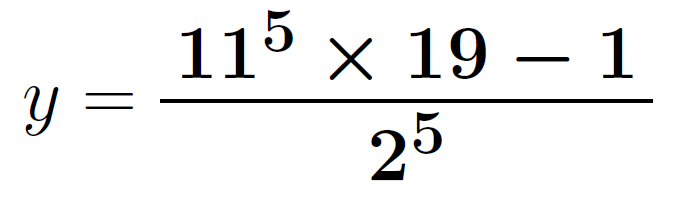
・・・・・・お・・・終わった・・・・・・
2022年共通テスト数学ⅠA総評
最後の最後に超弩級のモンスターを残して7年ぶりの伝説は幕を閉じた。
第4問の整数の5桁のマーク欄に恐れをなして第5問の図形を選択した受験生も多かっただろうが、こちらはこちらで普通に難しく、やはり5割以上取るのは容易ではない。
センター数学から究極変異を遂げた真・共通テスト数学は、非常に厳しい時間制限にも関わらず、通常のパターン問題演習のみで解ける問題は少なく、重厚な長文の割に丁寧な誘導はなく、大問・中問・小問とやたらと細々と分割した挙げ句に異なる分野の問題が混在し、「簡単かつ短時間で済む問題」「簡単だが時間がかかる問題」「難しいが短時間で済む問題」「難しく時間もかかる問題」を緻密なバランスと順序で配置して恐ろしく複雑な問題構成で受験生に難易度変化・分野変化・文章量変化・誘導量変化・計算量変化の激しい揺さぶりをかけ、センター数学の「一旦誘導に乗ったら最後まで一気にす~らすら~」のように一定のペースで解くことを許さない。ペースが乱れた受験生は、過去問演習で培ってきたタイムマネジメントが気付かないままに狂わされた上、巧妙に仕組まれた罠によって過去問演習で得た教訓を元に構築した戦略がことごとく裏目に出る。次第に追い詰められていき、正常な判断力は喪失、中盤のデータの分析で焦りと苛立ちが増幅、中盤以降は膨大な単純計算および無機質な反復によって気力も集中力も圧殺されて計算ミスや単純ミスが頻発、ミスしてもうまく穴にはまるような答えになる絶妙な問題作成によってその場でミスを修正することもかなわず1つのミスが所々で連鎖する。終いには、複雑な問題構成の中にさらに得点効率の高い問題と低い問題が入り乱れ、試験中に優先順位を正しく判断することは原理的に不可能、簡単な問題の配点は少なくされ、選択問題は複数完全解答を要求されるというシビアで癖がある凶悪な配点システムによって、過去問と同じような感覚でスコアマネジメントしていた受験生が、試験直後に「あ~いつも8割取れてるのに6割くらいしかできなかった・・・」とガックリ落ち込まされただけにとどまらず、さらに自己採点で「そ・・・そんな・・・40点しかない・・・なんでなんで・・・」という絶望のドン底にまで突き落とされたのだ。
つまり真相は
不可避の発狂である
2010、2013、2015年の伝説時は、受験生側の事前の対策や本番での対応の仕方次第では被害を最小限に抑えることが可能であったため、上位層への影響は限定的であった。
被害を受けた受験生側にも一定の責任・落ち度があったわけである。
しかし、2022年の受験生は究極変異体に不意打ちされた形であり、今回の惨劇には受験生側に落ち度はなかったといえよう。共通テスト数学対策のためのパターン問題演習・過去問演習・予想問題演習はほとんど役立たなかった(下手すると逆効果)といってよく、早い話どうしようもなかった。どのような既存の受験勉強をしてきていたとしても、最終的には「壊滅」という運命に収束する。
そう・・・今年の受験生は・・・
詰んでいたのだ
初めから
1997年センター数学史上最悪の浪人生ジェノサイド
2022年の受験生は、一言で言えば 運が悪かった。
ただ、不幸中の幸いで、全受験生が同じ試験を受けたのであるから公平といえば公平であった。自己採点後に絶望に打ちひしがれていた受験生も、平均点やボーダーラインの大幅低下を知って落ち着きを取り戻すことができたであろう。
まあ、数学が苦手な人が得をしたとかいろいろあるだろうが、それを言い出すとキリがない。50万人以上が受ける試験において100%の公平性などそもそもあり得ない。
実は、大きな制度変更があったとき、その割を受験生が食わされたのは初めてではない。
今から遡ること25年前の1997年にそれは起こった。
ⅠAⅡB方式に変わって初めてのセンター試験となったこの年、浪人生に配慮して行われたはずの旧課程対応の試験が新課程のものに比べて恐ろしく難しかったのだ。
| 現役生 | 数学ⅠA 66.40 | 数学ⅡB 63.90 | 計130.30 |
| 浪人生 | 旧課程数学Ⅰ 59.82 | 旧課程数学Ⅱ 42.21 | 計102.03 |
普段の外部模試で返却されたデータを見てみるとわかるが、同じ試験を受けた場合、現役平均に対して浪人平均は100点満点で10~15点ほど高くなるのが普通である。現役平均が130点ならば、浪人平均は150~160点になっていなければおかしい。
つまり、この年浪人生だけが数学で50~60点という絶望的なハンデを背負わされたわけである。
大学入試センターに「あまりにも不公平すぎる。得点調整すべきだ。」という批判が殺到したものの、当時の大学入試センター長は「浪人生の皆さん、社会人になったらもっと大変なことがありますよ~♪」と批判を一蹴した。結局、得点調整されることはなく、多くの二浪生を生み出した。
翌年以降、科目間で平均点に20点以上の差があった場合に得点調整が行われるようになったのであった。めでたしめでたし。
2022年共通テスト数学のデータでの振り返りと今後の予想
2022年共通テスト数学の最終的な平均点は、数ⅠA 37.96、数ⅡB 43.06 であった。
以下の駿台約30万人(ⅠA受験者は約35万人)のデータが、2022年の数ⅠAがいかに過酷であったかを如実に物語っている。
| ⅠA得点 | 2021年 (57.68) | 2022年 (37.96) |
| 100 | 1932人 | 56人 |
| 91-100 | 15702人 | 795人 |
| 81-100 | 46032人 | 4532人 |
約1万人いる大学受験の理系最上位層(最終的に東大理系・京大理系・国立医学部に合格)をもってしても、その半数は8割取ることを許されなかったのだ。
東京大学の合格者平均点(河合塾調べ)もご覧の通りである。
| 2021年 | 2022年 | |
| 理科一類 | 95 | 82 |
| 理科二類 | 91 | 77 |
| 理科三類 | 98 | 87 |
| 文科一類 | 88 | 69 |
| 文科二類 | 89 | 70 |
| 文科三類 | 84 | 64 |
冷静に分析してみると、数学的な難易度自体がそこまで高いわけではない。しかし、2022年の共通テスト数学からは、「平均点を50点にする」「上位層を駆逐する」という非常に強い2つの意思が感じられる。
平均層でも点を取れそうな問題が約50点分あるので50点までは割と取りやすいが、50点を超える辺りから急激に難易度と制限時間の壁に阻まれ始める。各大問の難易度・計算量・思考量があまり変わらないので、どの大問から手をつけたとしても結局は50点付近で行き詰まる。
それでも上位層は五合目以降を死に物狂いで登っていくが、頂上はおろか八合目にすらたどりつけずに力尽きていく。死闘の痕跡が残る上位層受験生の問題用紙を見せてもらうと結構泣ける。(´;ω;`)ウッ…
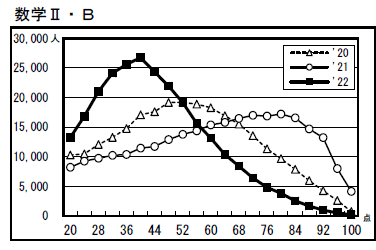
そして、過去ダントツ最低の平均点となったⅠAに隠れているが、ⅡBも準伝説レベルの難度であった。
| ⅡB得点 | 2021年 (59.93) | 2022年 (43.06) |
| 100 | 4137人 | 182人 |
| 91-100 | 28612人 | 2008人 |
| 81-100 | 69326人 | 8473人 |
こちらもⅠAと同様、4,50点までは割と取りやすいが、高得点を取るのは至難の業である。
どれほど高得点を取ることが困難であったのかが度数分布に現れている。なお、ⅠAの最頻は30点である。

今後はいかに
2023年以降がどうなるかは蓋を開けてみなければわからない。
しかし、「平均点を50点にする」「上位層を駆逐する」という作問のスタンスが大きく変わるとは思えない。
2021年の平均が想定を上回ったせいなのか、2022年ⅠAはさすがにさじ加減を間違えてやり過ぎてしまった感が否めないが、試験時間が100分とは言わないまでもせめて90分あったならば、45点ほどの平均点に落ち着き、ほぼ想定通りということになっていたのではないか。
そして、ⅡBは多少下振れしただけで、これでほぼ狙い通りなのではないか。今年に限っては、ⅠAで心が折られたせいもあったかもしれない。
上位層であれば8割9割簡単に取れる時代は終わったように思える。
それでも、試験である以上は対策が可能であるから、万が一2023年以降に2022年と同レベルの問題が出題されたとしても、2022年の平均点よりは高くなるはずである。
2022年受験生の犠牲を無駄にしてはならない。
2012年センター数学ⅠA vs 2022年共通テスト数学ⅠA 驚愕の難易度差
2022年共通テスト後、平均点速報を聞いてここぞとばかりにマウントを取りに来た大人に「今年の受験生は努力不足」「ⅠAなんて9割余裕」「パターン暗記ばっかりやっているから自業自得だ」「読解力が足りない」などと好き放題に煽られてしょんぼりしている受験生も散見された。
老害を煽り返そうではないか。
2022年ⅠAが第4問までで20ページ(2021年は24ページ)であったことを踏まえた上で2012年の問題を見てみるとその差は歴然であり、2022年現在25歳以上の大人が好き勝手抜かしていても、もはや老害の戯言でしかない。
「おいおい、嘘だろwwww2012年のⅠAたったの8ページwwwてか実質5ページwwwww教科書レベルの問題多杉www頂点求めただけで4点wwwしかも勘で当たりまくるwwwこんなんで9割自慢してたのかよwwwwwゆとりってレベルじゃねーぞwwwwwwwww」
よりわかりやすい比較は以下の記事で。
どんだけ増やすねんヽ(`Д´)ノ
最後に
2022年、今年の高校新1年生から教育課程が10年ぶりに大きく変わる。
これに対応して、2025年の共通テストからは以下のように変わる(2022年現在未確定)。
- 数ⅡBが数ⅡBCになり現在の60分から70分に増加。(数Cは現行の数Bベクトル・数Ⅲ複素数平面・数Ⅲ平面上の曲線)
- 国語は現在の80分から90分に増加。
- 国立大受験では新教科「情報Ⅰ(プログラミング)」(60分)を加えた6教科8科目が課される。
未来の受験生南無阿弥陀仏(-人-)
新課程用の青チャートの表紙カッコイイ♪