2020年 横浜市立大学　無理数の無理数乗が有理数？驚異の両刀論法

受験で稀に問われて即答が難しいのが以下である。

1. 有理数の有理数乗は有理数か無理数か(数Ⅱ)。
2. 無理数の有理数乗は有理数か無理数か(中学)。
3. 有理数の無理数乗は有理数か無理数か(数Ⅱ)。
4. 無理数の無理数乗は有理数か無理数か(数Ⅱ)。

1.と2.は少し考えるとすぐにわかるが、3.と4.がいきなり問われるとかなり難しく、具体例を覚えておくことが望ましい。

まとめてみると以下のようになる。

このように、3.と4.では、対数を利用した具体例を示す必要があり、あらかじめ知っていないとかなり厳しいわけである。

実は、4.の無理数の無理数乗が有理数になりうることの証明については、上の具体例を示す方法以外に非常に面白い方法が知られており、2020年の横浜市立大学医学部で出題された。

2020年横浜市立大学医学部の問題

(1)は以下に注意した上で計算する。(2)は基本問題である。

さて、本題は(3)である。

まず、(1)の誘導がない場合の解答例を示す。初見ならば、誘導を無視してこのように解答するのが実戦的である。

次に、問題作成者が意図していた解答を示す。

驚くべきことに、 √2^√2 の正体が不明のまま、x^yが有理数になる無理数の組(x,y)の存在だけは示せてしまうのである。

初見でこの両刀論法に気付けた受験生は何人いただろうか。

多くの受験生は、√2^√2 が無理数であることの証明を試みるも失敗し、「(1)より明らかに存在する」などと適当にごまかした解答を作成する羽目になっただろう。

自分が2015年頃にネットでこの証明を初めて知ったとき、以下が思い浮かんだ。

このような論理パズルを彷彿とさせるような方法によって数学の命題を証明できるという受験数学では極めて珍しい出題であった。

論理パズルが好きな人はこちらもどうぞ。

無理数判定の難しさ

一般に、√2やlog₂3のような単純なものを除けば、ある数が有理数か無理数かを判定するのは非常に難しい。

円周率は紀元前から考察の対象とされてきたが、その無理数性が証明されたのは1761年のことである。現在は初等的な方法も知られており、大学入試での出題例もある。

また、高校数学の2大定数のもう1つである自然対数の底eの無理数性の証明は、1744年に18世紀最大の数学者レオンハルト・オイラー(スイス)による。

しかし、以下のように単純な構造で直感的には無理数にしか思えない数ですら、2022年時点でも有理数なのか無理数なのかはわかっていない。

無理数のように見えても、横浜市立大学の(1)のように実は整数などということもありえるので、当然ながら証明されるまではその正体は闇に隠れたままである。おそらく無理数だとは思うが、万が一有理数ならば(整数)/(整数)で表せるということになるので、個人的には有理数であってくれた方が面白いと思っている。

なお、上で登場した √2^√2 については、1934年に証明された以下のゲルフォント＝シュナイダーの定理により、その正体が判明している。

「αを0, 1以外の代数的数、βを有理数ではない代数的数としたとき、α^βは超越数である。」

有理数係数代数方程式の解となる数を代数的数、ならない数を超越数という。例えば、√2は x²-2=0 の解なので代数的数である。代表的な超越数はπとeである。超越数であることの証明は無理数であることの証明よりもさらに難しく、eの超越性の証明は1873年シャルル・エルミート(フランス)、πの超越性の証明は1882年フェルディナント・フォン・リンデマン(ドイツ)による。

ゲルフォント＝シュナイダーの定理により、√2^√2 は超越数であることがわかる。

超越数ならば必ず無理数である(√2のように逆は成り立たない)から、√2^√2 は無理数である。

ちなみに、ゲルフォント＝シュナイダーの定理とオイラーの公式から、ゲルフォント定数e^πについては超越数、つまりは無理数であることがわかる。

オイラーの公式 e^ix=cosx+isinx より

e^π=(e^iπ)^-i=(cosπ+isinπ)^-i=(－1)^-i

－1と－iはゲルフォント＝シュナイダーの定理の前提条件を満たすから、(－1)^-i、つまりe^πは超越数である。

√2の無限指数タワー(テトレーション)

関連して、以下の数についても触れておくとしよう。

√2^√2 の正体ですら高校数学の範囲を超えていたのだから、「√2の無限指数タワーの正体なんて高校数学の遙か先にあるのではないか」と思ったかもしれない。

しかし、意外なことに無限の場合は高校数学の範囲内なのである。

無限指数タワーは、底aが以下のような範囲の場合に収束することが知られている。この証明も18世紀最大の数学者レオンハルト・オイラー(スイス)による。

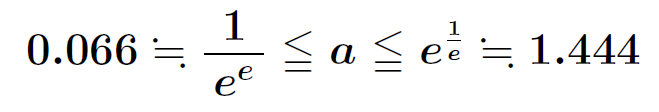
√2≒1.414であるから、√2の無限指数タワーは収束する。

その収束値を求める問題が、2011年に同志社大学で出題された。数Ⅲの極限と微分法の知識を要する。

(3)までは基礎的だが、(4)以降は同種の問題(解けない漸化式の極限の問題)の経験が必要である。