
2015年、センター試験数学ⅡBにおいていわゆる「7倍角の伝説」が誕生した。
当然、当カテゴリでも取り上げている。
上の記事はかなり長いので、7倍角に関する部分を要約する。
受験数学で暗記が推奨されるのは、せいぜい3倍角の公式までである。
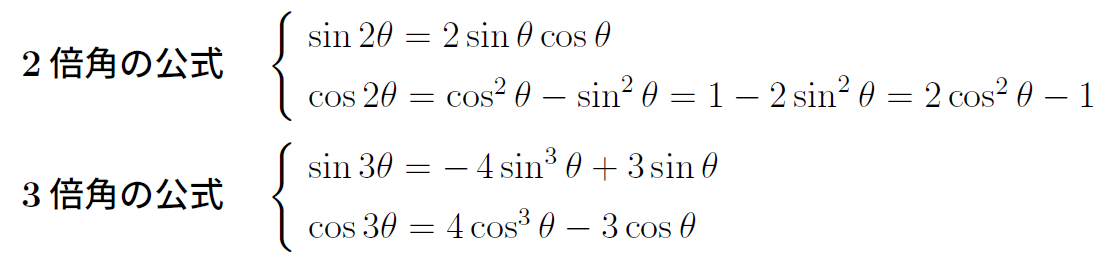
しかし、2015年センター数学ⅡBでは以下の数式が登場し、多くの受験生は手も足も出なかった。
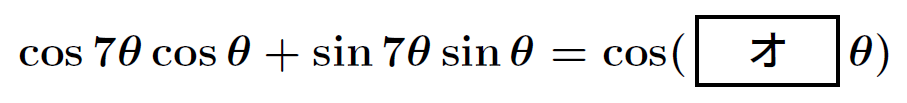
「7倍角なんてどうすればいいの・・・(´;ω;`)」
実際には、「7」という数字に特別な意味合いはなく、本質を理解してさえいれば7だろうが100だろうが難なく対応できる。
しかし、特に文系はこのsin7θやcos7θがあたかも2倍角の公式や3倍角の公式の延長線上にしかない式であるかのように錯覚し、試験後に「7倍角が出た」とネットで大騒ぎになったのである。
数Ⅲを学習した理系ならば、数Ⅲでsinπθなんてものまで登場するので7θを見たところで大して何も思わないし、普通はあえて「7倍角」と表現することはない。
「7倍角」と表現することがあるとすれば7倍角の公式を導出したり利用したりする場合であるが、7倍角はおろか、5倍角の公式ですら必要になることは稀である。
「常識で考えれば7倍角の公式が入試で出るわけないだろうに・・・┐(´∀`)┌」
などと思った数学が得意な人も多かったかもしれない。
ところが、翌年2016年に横浜市立大学で以下の問題が出題された。

で、出た~!!!
正真正銘の7倍角!!!
7倍角の伝説が誕生した直後の7倍角の公式の導出、これもまた伝説と呼ぶにふさわしい出題である。
ということで、「ド・モアブルの定理(複素数平面)を用いて」という誘導に素直に従って7倍角の公式を導出してみよう。

こうして、7倍角の公式(sinθとcosθの7次式)が導かれる。
単に7倍角の公式を導くだけならば、sin(4θ+3θ)として三角関数のみの知識で導くことも可能だが、見かけが異なる式が導かれて(2)との関連がわからなくなってしまう。そのための誘導である。
もっとも、真の7倍角の公式は、以下のようにsinθのみで表現したものになるだろう。実部の比較により求まるcos7θの方も示しておく。

当然ながら無意味に7倍角の公式を導いたわけではなく、(3)が最終目標である。
(2)と(3)の解答も示しておく。普通に良問である。

本問を一般化すると、伝説のバーゼル問題が解決できる。それを元にした出題が2018年の東海大学でなされている。
伝説が伝説を呼び、さらなる伝説へ。



