2017年 慶應義塾大学　解答奉納！江戸の数学『和算』を謳歌する!!!

2017年、慶應SFC環境情報学部の第1問では、何やら古めかしい用語が使われており、また中学入試や高校入試にありそうな図が目を惹いた。

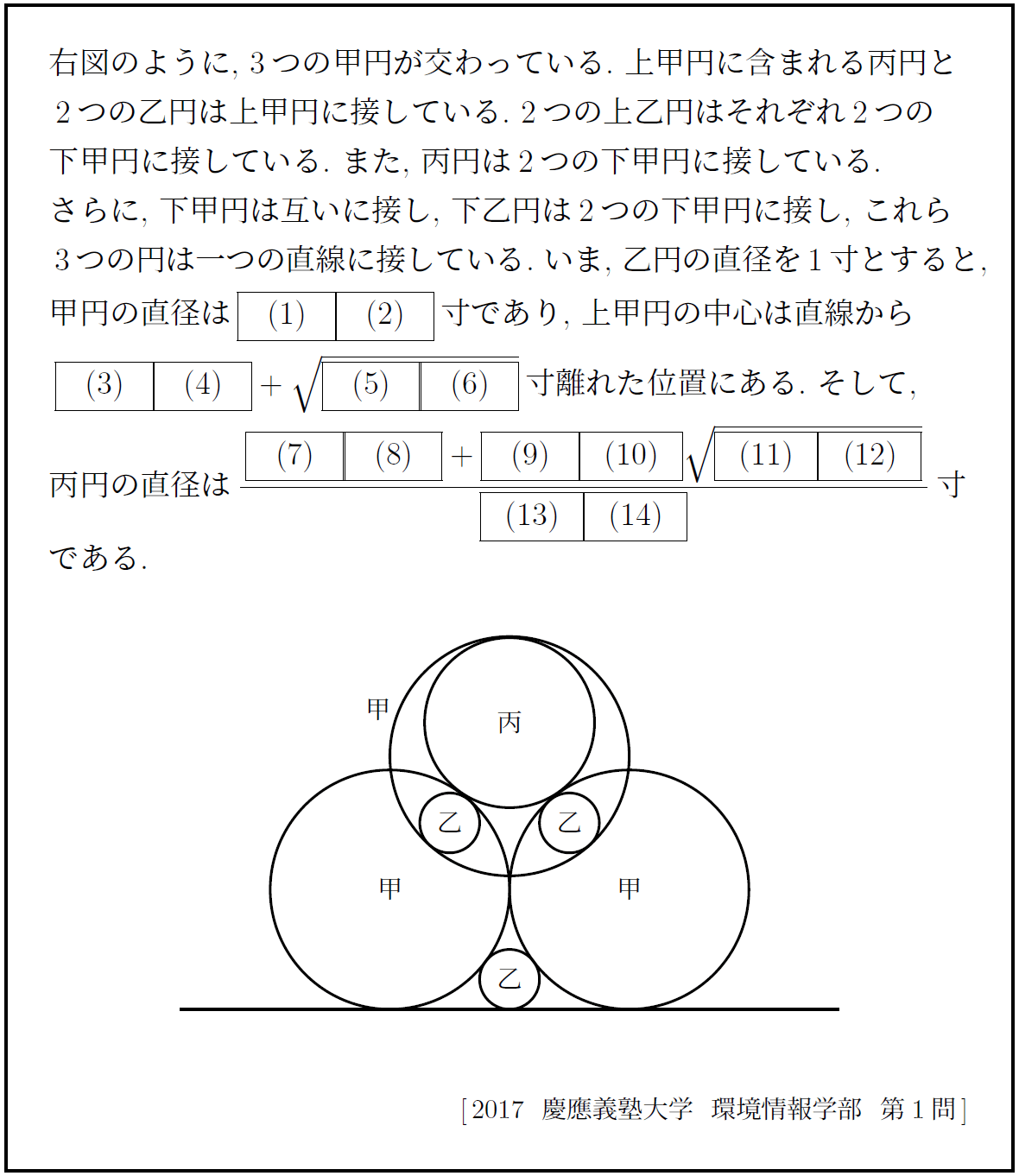
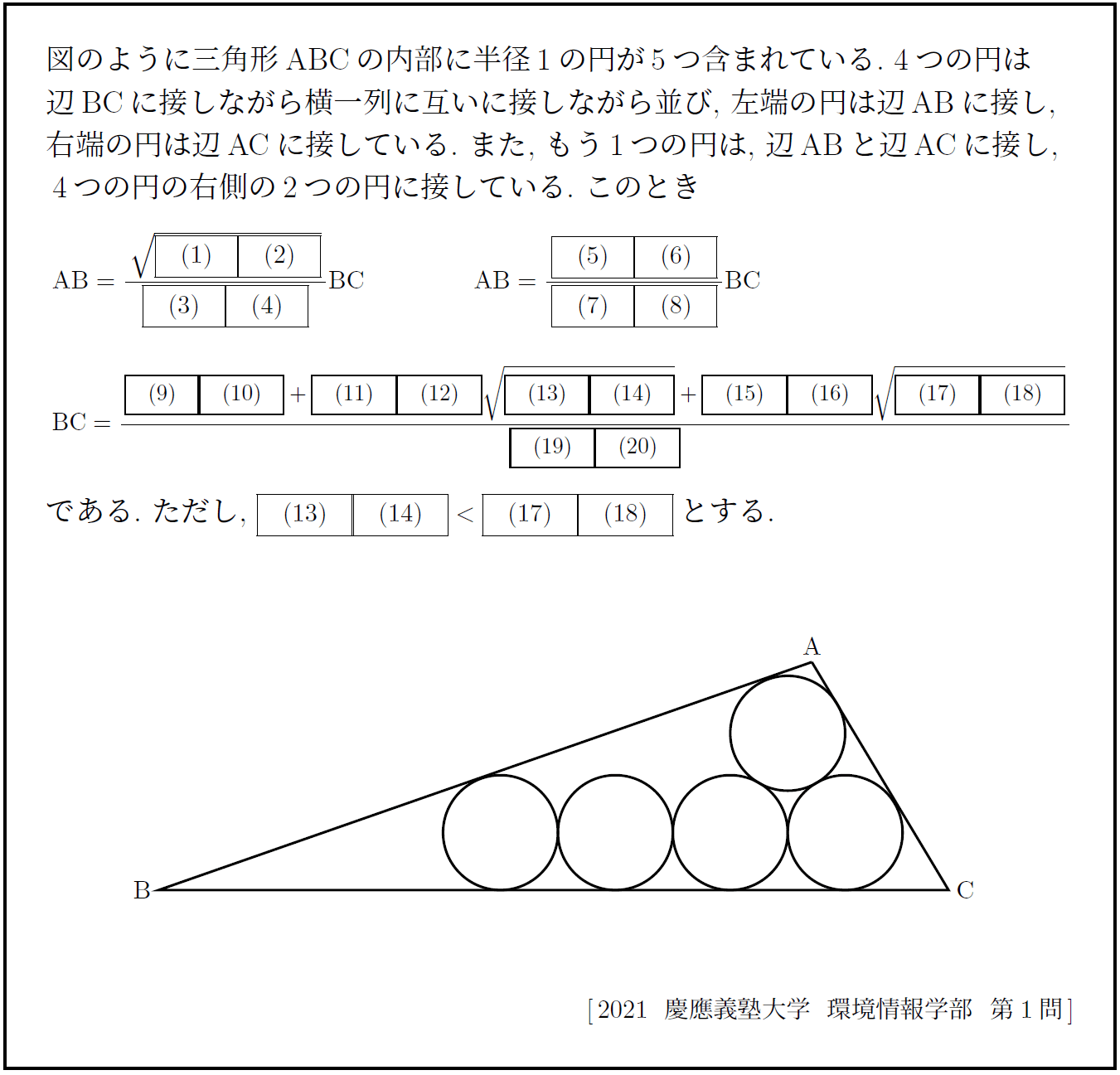
注　「上甲円と下甲円の共通部分に含まれる乙円は最大円とする」という指定がない場合には図のようになるとは限らず、この問題の不備のために(3)～(14)は全員正解の扱いとなった。

本問は、江戸時代の数学『和算』にちなんだ問題である。和算の問題には、このように多数の円が絡む幾何の問題が多い。

すべて当時のような文言で解答すると訳が分からなくなるので、雰囲気を味わえる程度の解答を奉納する。乙円は最大円として考えた。

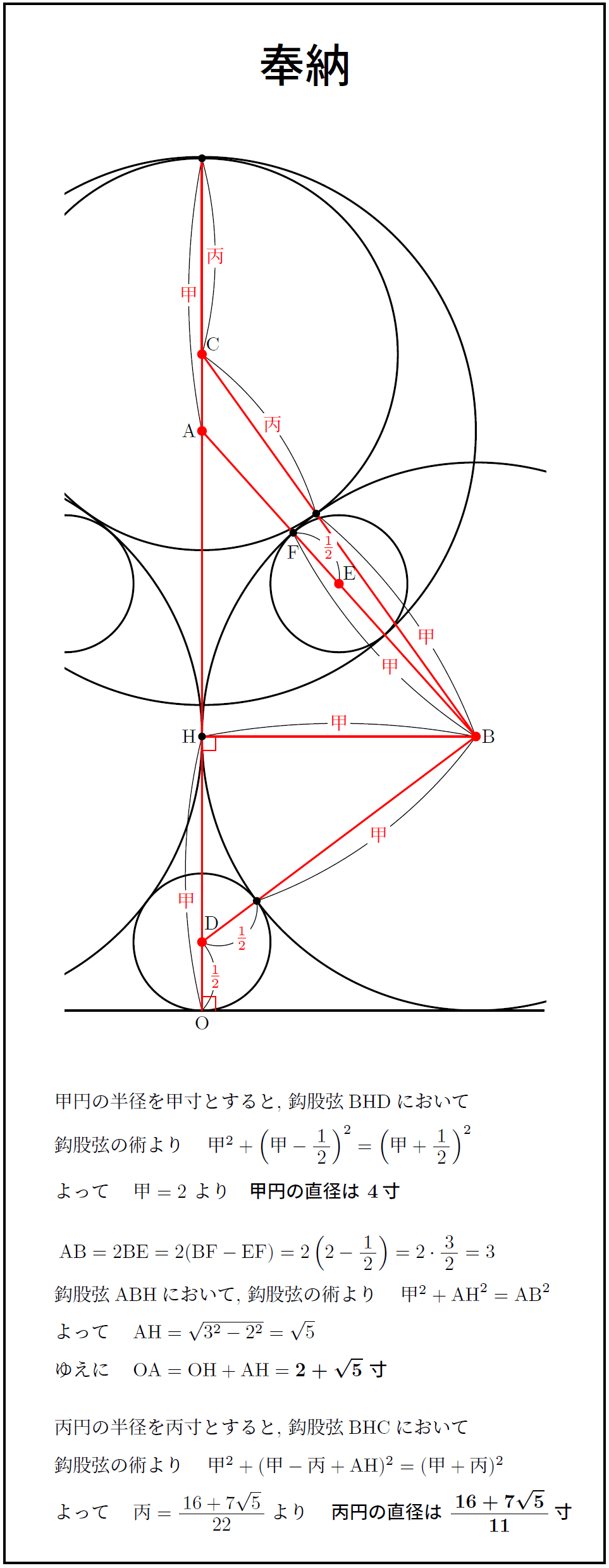
和算では、直角三角形において、直角を挟んで短い方の辺を鈎こう、長い方の辺を股こ、斜辺を弦げんといった。

センター試験でもあったが、円の直径を問われたときに半径を答えるミスが多発するので注意が必要である。

和算の歴史

「和算」は日本の数学の源流でありながら、ほとんどの人がその歴史を知らないのは残念なことである。

以下で、約200年の和算の歴史を紹介するとしよう。ただし、200年という長い歴史をすべて語ろうとするとキリがないので、大まかな流れと特に有名なエピソードに限定して紹介する。

江戸時代の教育システム

慶長5年(1600年)の天下分け目の決戦「関ヶ原の戦い」で勝利した徳川家康は、慶長8年(1603年)に征夷大将軍となり、江戸に幕府を開いた。265年続くことになる江戸時代(1603-1868年)の始まりである。

長く続いたということは、端的に言えば「平和と安定」の時代であったということである。大飢饉、富士山噴火、宝栄地震のように自然災害は多発したものの、大きな戦争はなく、1639年にキリスト教の布教を畏れた幕府が始めた鎖国によって異国からの文化移入もなく、江戸の教育・文化・娯楽は日本独自の発展を遂げる。

浮世絵、俳諧、歌舞伎、人形浄瑠璃、相撲、･･････

これらの江戸の文化については中学校の日本史でも学習するわけだが、江戸時代の前期から後期の長きに渡ってブームが続いた文化についてはなぜかあまり触れられない。

それこそが

数学

数学の発展と普及に大きな役割を果たしたのが「寺子屋」である。

寺子屋は、庶民の子供に主に読み・書き・算盤(そろばん)を教える私設の教育機関であり、その起源は中世に寺院が庶民の世俗教育を担当していたことにまで遡ることができる。近世に入ると教育が寺院で行われることはなくなったが、寺院に住み込みで学習する子供たちが寺子と呼ばれていたことから、教育施設を寺子屋と呼ぶようになった。

寺子屋は、幕末期には全国各地に存在し、明治時代初期に設置された小学校の母体となった。日本の人口が約3000万人の幕末期に全国に1万5千軒以上の寺子屋があったとされ、少子化とはいえ人口1億2千万人の現在の小学校が約2万軒であることを考慮すると、かなり広く教育が行き届いていたことがうかがえる。

一寸子花里「文学ばんだいの宝」, Public domain, via Wikimedia Commons

寺子屋は義務教育ではなく、試験も受験もない。出席も欠席も自由で、学びは遊びの一環であった。幅広い年齢層の子供がいて、一律の集合教育ではなく、師匠が各子供の親の職業や本人の希望を汲み取ってカリキュラムを作る個別教育がなされた。当時、一般庶民や女性まで教育を受けることができたのは、世界的にも珍しいことであった。

吉田光由『塵劫記』

徳川幕府の安定した治世の下である程度教育が行き届くと、教養、情報、そして娯楽を求めて読書への欲求が高まっていった。

江戸時代には井原西鶴『好色一代男』、十返舎一九『東海道中膝栗毛』、曲亭馬琴『南総里見八犬伝』などがベストセラーになったが、これらが売れたのはあくまでも長い江戸時代の内の一時期のみである。

一方、江戸時代の全期間に渡って売れ続け、文学作品を遙かに凌ぐ部数を売り上げた書籍が存在した。

吉田光由よしだみつよし『塵劫記じんこうき』

塵劫記は、和算家の吉田光由(1598-1672)が寛永4年(1627年)に出版した算術入門書である。

それ以前にも算術書はあったが、無機質なものばかりであった。塵劫記は、四則演算、そろばんの使い方、田畑の面積の量り方、測量術といった日常生活に役立つ実用性のある問題に加えて、鶴亀算、継子立て、ねずみ算といった数学パズルのような問題まで幅広く網羅されており、さらに丁寧な説明や豊富なイラストつきという高い完成度が好評を博した。

難易度順に並べられた構成は学習用にも優れており、寺子屋の教科書として利用された。解説本や海賊版も出版され、『塵劫記』と名のつく本は300年間で400タイトルにもなったという。

国立国会図書館デジタルコレクション

この塵劫記の出版をきっかけに、世界でも他に例を見ない日本独自の数学文化『和算』が始まったとされる。

上は将軍・藩主から下は農民・町人まで、年齢も身分も男女も分け隔てなく、数学を一種の娯楽として楽しんでいたのである。

遺題継承と算額奉納

塵劫記が普及するにつれて、大した能力もないのに教師を名乗って勝手に塾を開く輩が現れ出した。

そこで、吉田光由は寛永18年(1641年)出版の『新篇塵劫記』において、下巻に「遺題」と呼ばれる解答のない難問12問を掲載した。「教師を名乗る人がいれば、遺題を解かせてみてその力量を試してみるとよい。」という吉田の意図であった。ただし、遺題の中には4次方程式を解くことが必要な難問も含まれており、掲載当時は誰も解けなかった。

難問があれば挑戦したくなるのが人の性、庶民達は競い合うように遺題に挑み、和算家達は解答を自分の書籍の中で発表した。その書籍には解答だけでなく新たな問題も追加されていて、それをさらにまた別の人が挑戦するという循環が起こった。中には、150題以上もの遺題が収録された書籍もあったという。これが200年近くにわたって続いた「遺題継承」である。

また、大型の絵馬に問題と解答を描いて神社仏閣に奉納する者も現れた。これが「算額奉納」の始まりである。問題が解けたことを神仏に感謝し、また、研究発表の場でもあった。

Momotarou2012, CC BY-SA 3.0, via Wikimedia Commons

算額には、多くの人の目を惹きつけることができるような幾何の問題が多い。ほとんどは現在の中学数学・高校数学レベルであるが、ソディーの六球連鎖の問題や、シュタイナー環の問題など、西洋数学に数十年先駆け当時世界最高レベルに達していたものもある。ソディーの六球連鎖に至ってはヨーロッパで発表されたのが20世紀半ばであるから、100年以上先駆けていたことになる。

最も古い算額は、第5代将軍綱吉の時代の天和3年(1683年)の算額とされる。その後は増え続け、最盛期の1800年代から幕末までの約60年間には全国各地で毎年20面以上の算額が新たに奉納された。かつて存在した2600面のうち約900面の算額が全国各地に現存している。

以下のサイトには全国の現存する算額がまとめられており、意外と身近な神社仏閣に残っていることがわかる。

和算の館

1639年に始まった鎖国によって西洋の影響と切り離された時代、遺題継承や算額奉納という日本特有の現象のもとで和算家達がお互いに切磋琢磨していくことで、「和算」は高等数学にまで独自の発展を遂げていった。

和算の大家・関孝和

裾野が広がるほど、その中から天才が生まれる可能性が高くなる。

17世紀後半、和算ブームの中から世界的な天才数学者が誕生した。「算聖」とも謳われた関孝和せきたかかず(1640年頃-1708)である。

upload by AMorozov, Public domain, via Wikimedia Commons

和算の根底は、中国から伝わった「天元術」にある。この天元術を初めてマスターしたとされるのが、和算家の沢口一之である。1670年、沢口は天元術を用いて当時難問であった遺題を解き、『古今算法記』に掲載した。さらにこの中で、天元術では解けない遺題を15題掲載した。

天元術とは、算木や算盤を用いた高次方程式の数値解法である。何次方程式でも対応できる優れモノであったが、扱える変数はxの1つのみであった。『古今算法記』の遺題はどれも多変数方程式を必要とする問題で、当時は誰も解くことができなかった。

関孝和は、算木や算盤を使わずとも、計算を紙の上だけで行えるよう「傍書法(筆算)」を発案し、多変数方程式を表した。さらに、天元術を拡張し、多変数連立方程式を解くための「点竄術てんざんじゅつ」を発明した。これは西洋数学における代数学に相当するもので、関孝和の最大の功績の1つである。点竄術によって和算は中国数学を凌駕して独自の発展を始め、やがて部分的にではあるが西洋数学をも凌駕することになる。

延宝2年(1674年)、関孝和は点竄術を用いて『古今算法記』の遺題をすべて解いて『発微算法』で発表したことにより、事実上和算の第一人者となった。『発微算法』はかなり説明不足であったために当初は理解されなかったが、弟子の建部賢弘たけべかたひろの『発微算法演段諺解はつびさんぽうえんだんげんかい』(1685年)における詳細な解説により、点竄術の真髄が広まることになった。

1681年、関は暦の作成にあたって円周率の近似値が必要になったため、正131072角形を使って小数第16位まで算出した。海外では1610年までには小数第35位まで求められていたが、関は少ない計算量で近似値の精度を高めることができる、現在では「エイトケン加速」と呼ばれる方法を世界で初めて編み出して求めたことが特筆される。西洋でエイトケン加速が再発見されたのは1876年であったから、約200年先んじたことになる。

この他にも、関は「ニュートンの近似解法」「ニュートンの補間法」「極大極小理論」「終結式と行列式」「近似分数」「ベルヌーイ数」「パップス・ギュルダンの定理」「円錐曲線論」「球面三角法」など、多くの業績を残した。中でも、行列式は世界に10年、ベルヌーイ数は世界に1年先駆けての発見であった。

関が存命中に出版したのは『発微算法』1冊に留まったが、それ以外の膨大な研究成果は建部兄弟に代表される弟子達によってまとめられ、後世に関の偉大な功績を伝えることになった。

和算の衰退と近代教育の幕開け

和算については、関孝和を初めとする多くの和算家の活躍もあり、西洋数学に匹敵していたという趣旨で語られることが多いが、決定的に劣っていたのも事実である。

関数や座標の概念がなく、記号の改良が不十分で、論証や体系的理解も乏しかった。また、図形問題に大きく偏り、自然科学への応用もなされなかった。流派ごとに発展し、秘密主義・派閥主義の影響で重要な研究結果を奥義として公開を控えることもあった。

鎖国下で独自の発展を遂げてきた和算であったが、必然的に来るべきときが来る。

ペリー提督率いる黒船来航(1853年)

圧倒的な軍事力によって「開国か攘夷か」の2択を迫られた日本は、その後の15年間、動乱の幕末を迎える。

1868年に江戸時代が終わり明治時代に入ると、明治新政府は、富国強兵と殖産興業をスローガンにあらゆる面で西洋化を進めた。西洋化は、軍隊の近代化や学制の改革に留まらず、暦と度量衡にまで及んだ。

そして教育においては、明治5年(1872年)に「和算廃止、洋算専用」とする指針が策定され、翌年から小学校教育が始まって日本の近代教育の幕が開けた。代替がないそろばんだけは存続することになったが、和算は公教育の現場からは姿を消した。

初期の小学校教育は和算家によって行われたが、各地に教員養成学校が設立されてその卒業生たちが教壇に立つようになると、和算家の社会的な役割も年を追うごとに小さくなっていき、20世紀に入る頃には、和算は完全に過去の遺物と見なされるようになった。

明治10年(1877年)には、日本初の大学「東京大学」が設立された。東京大学は1886年の帝国大学令に基づいて「東京帝国大学」となり、その後は京都・東北・九州・北海道・大阪・名古屋にも帝国大学が順次整備されていった。現在、かつての帝国大学は「旧帝大」と呼ばれ、受験業界では東京工業大学・一橋大学と合わせて上位難関国立大学に位置づけされている。

最後に

「江戸時代、日本の教育や識字率は世界トップクラスだった」とするサイトや書籍も多い一方、それは大袈裟すぎるという研究もあり、諸外国との比較の確定的な見解はない。国際基準がなかった時代の正確な比較などそもそも無理がある。

いずれにせよ、かつての日本には、独特の数学文化が存在し、その中から関孝和を初めとする多くの和算家が誕生して大いに数学が盛り上がった時代があったことは疑いようのない事実である。

受験数学に忙殺される現代、たまには娯楽数学を興じた過去の日本人に思いを馳せてみるのもよいのではないだろうか。

実は、最近の慶應SFCの入試では、2017年以外にも和算を匂わせる問題が複数出題されている。

これを遺題としておいておく。難易度は様々である。

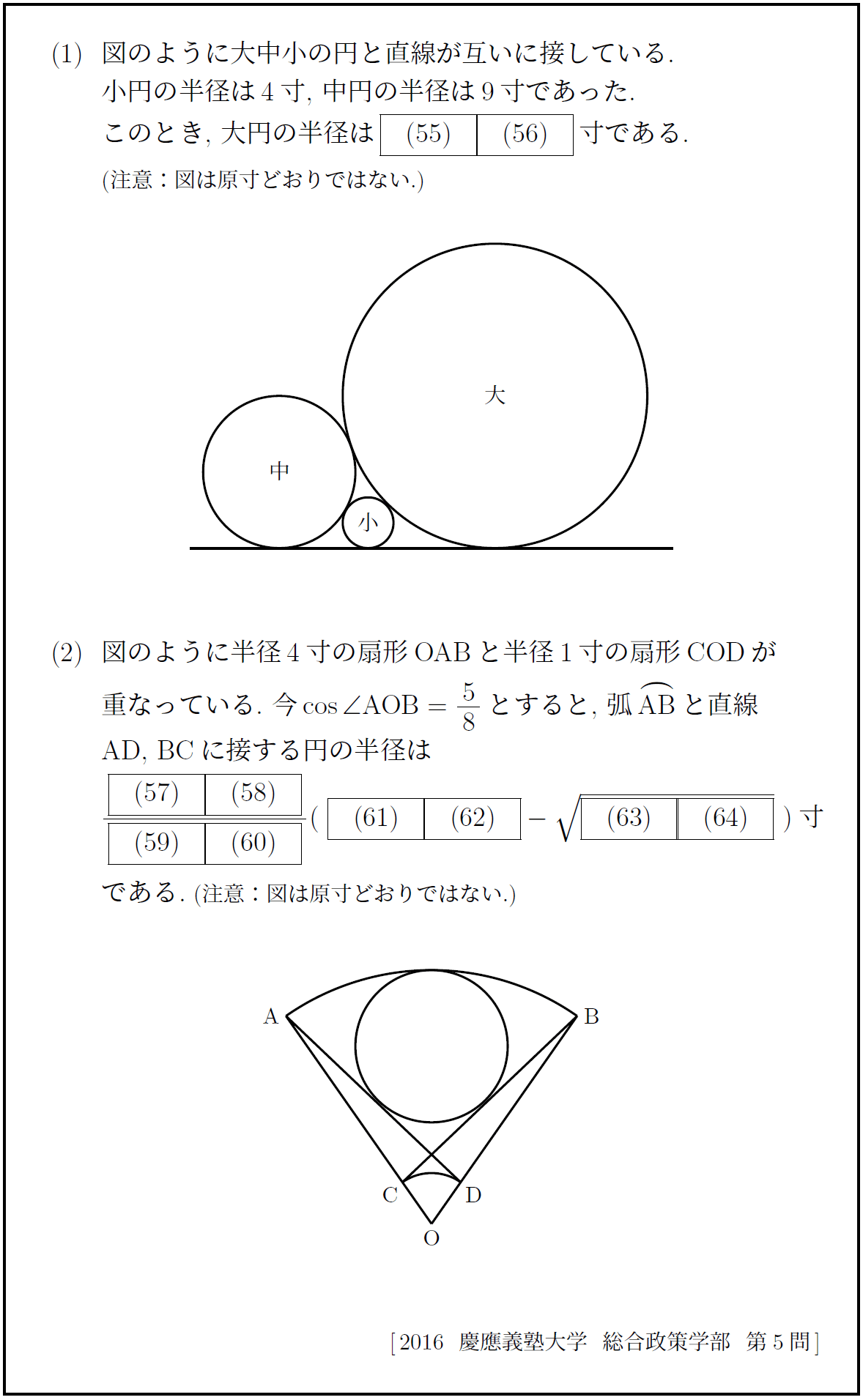
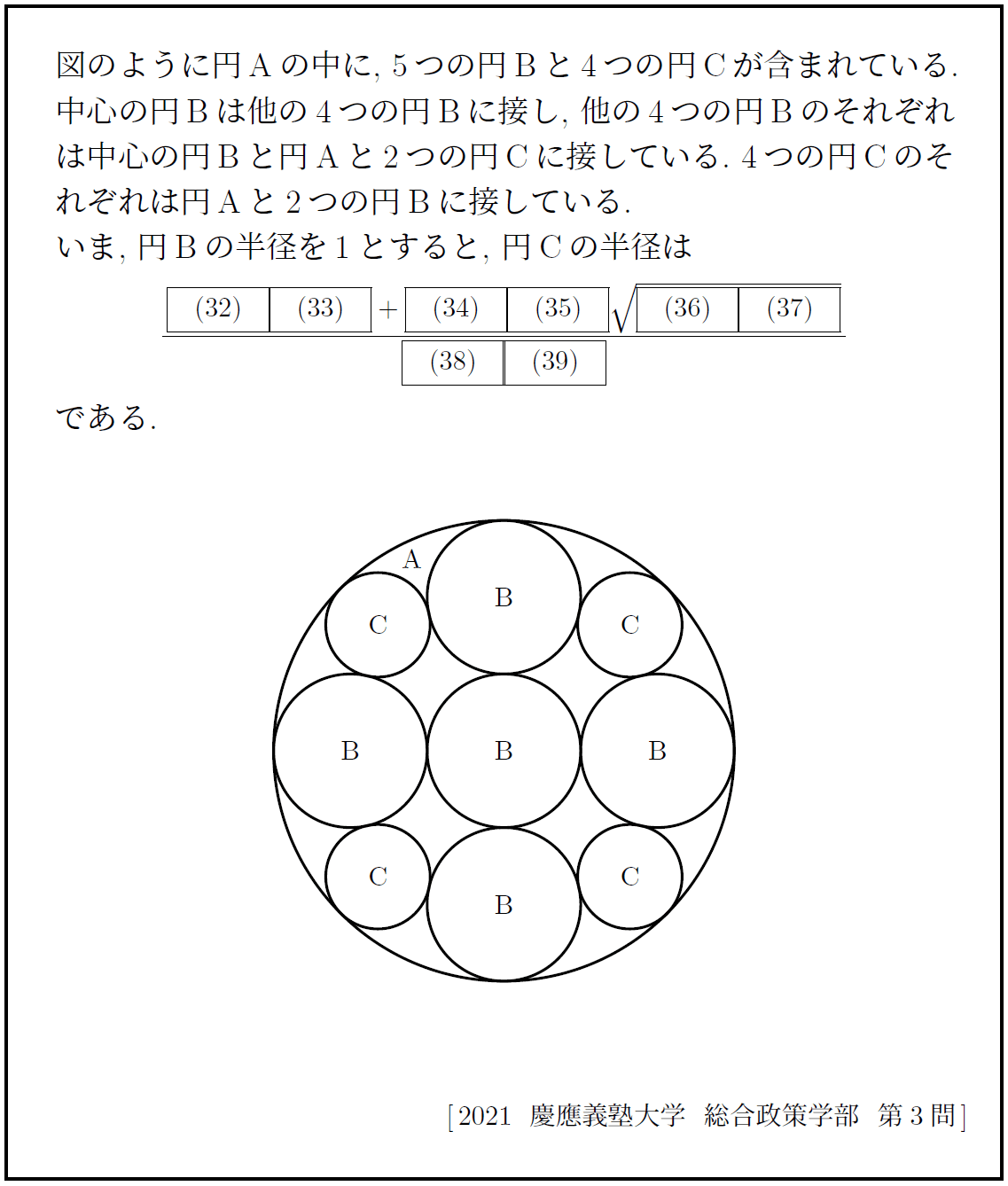
確認のための解答くらいはつけておくかな。

　

また、「和算」という先人達の偉大な遺産を継承すべく、博物館などを中心に様々な活動が行われている。

例えば、岩手県の一関市博物館では毎年和算の問題を出題しており、小学生から100歳近い高齢者まで1000人以上が応募している。次回チャレンジしてみては？

和算に挑戦 | 一関市博物館

参考文献